Updated: 9 August 2010
Use NEGBINOMDIST to calculate the negative binomial distribution. NEGBINOMDIST returns the probability that there will be k failures before the rth success, when the constant probability of a success is p. The formula for the negative binomial distribution is:
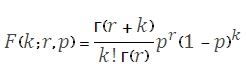
Where
k is the number of failures
r is the number of successes
p is the probability of a success
Syntax
SELECT [wctStatistics].[wct].[NEGBINOMDIST] (
<@Number_f, float,>
,<@Number_s, float,>
,<@Probability_s, float,>)
Arguments
@Number_f
is the number of failures. @Number_f is an expression of type float or of a type that can be implicitly converted to float.
@Number_s
is the number of successes. @Number_s is an expression of type float or of a type that can be implicitly converted to float.
@Probability_s
is the probability of a success. @Probability_s is an expression of type float or of a type that can be implicitly converted to float.
Return Types
float
Remarks
· If @Probability_s <0 or @Probability_s > 1, NEGBINOMDIST returns an error.
· If @Number_f < 0 or @Number_s < 1, NEGBINOMDIST returns an error.
· NEGBINOMDIST = BINOMDIST(@Number_s,@Number_f+@Number_s,@Probability, 'False')*@Number_s/(@Number_f+@Number_s)
Examples
SELECT wct.NEGBINOMDIST(4,90,0.975)
This produces the following result
----------------------
0.116820452331376
(1 row(s) affected)
SELECT wct.BINOMDIST(90,90+4,0.975, 'False')*90/(90+4)
This produces the following result
----------------------
0.116820452331368
(1 row(s) affected)
select wct.BETADIST(0.975,90,4+1,NULL,NULL)-wct.BETADIST(0.975,90,4,NULL,NULL)
This produces the following result
----------------------
0.116820452327232
(1 row(s) affected)