SKEWNESS_P
Updated: 24 May 2013
Use the aggregate function SKEWNESS_P to calculate the skewness for an entire population. The SKEWNESS_P function is an implementation of the skewness as formulated by Abramowitz and Stegun in Handboook of Mathematical Functions, 26.1.15.
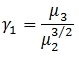
Syntax
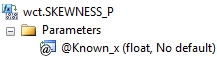
Arguments
@Known_x
the values to be used in the calculation. @Known_x must be of a type float or of a type that implicitly converts to float.
Return Types
float
Remarks
· If you want measure the skewness for a sample, then use the SKEWNESS_S function.
· To calculate the population kurtosis use the KURTOSIS_P function.
· To calculate the sample kurtosis use the KURTOSIS_S function.
Examples
SELECT wct.SKEWNESS_P(x) as SKEWNESS_P
FROM (
SELECT 30000.0000216303 UNION ALL
SELECT 30000.0000565854 UNION ALL
SELECT 30000.000038137 UNION ALL
SELECT 30000.0000495983 UNION ALL
SELECT 30000.0000185861 UNION ALL
SELECT 30000.0000863479 UNION ALL
SELECT 30000.0000776366 UNION ALL
SELECT 30000.0000637985 UNION ALL
SELECT 30000.0000939786 UNION ALL
SELECT 30000.000031191 UNION ALL
SELECT 30000.0000550457 UNION ALL
SELECT 30000.0000207558 UNION ALL
SELECT 30000.0000805531 UNION ALL
SELECT 30000.0000241287
)n(x)
This produces the following result
SKEWNESS_P
----------------------
0.204132079810574
In this example, we generate 100 random numbers form the standard normal distribution using the wct.SeriesFloat function and calculate the population skewness.SELECT wct.SKEWNESS_P(k.SeriesValue) as SKEWNESS_P
FROM wctMath.wct.SeriesFloat(0,1,NULL,100,'N')k
This produces the following result (your results will be different).
SKEWNESS_P
----------------------
-0.143810928339362