Updated: 21 July 2017
Use the SQL Server scalar function STIRLING2 to calculate the Stirling numbers of the second kind. The Stirling numbers of the second kind count the number of ways to partition n elements into k nonempty sets:
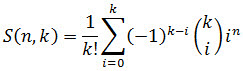
Where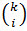 
is the binomial coefficient (see BICO).
Stirling numbers of the second kind exhibit the following recursive relationship.
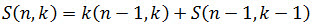
Syntax
SELECT [wct].[STIRLING2] (
<@n, int,>
,<@k, int,>)
Arguments
| Input Name | Definition |
| @n | Number of items |
| @k | Number chosen |
Return Type
Remarks
- If @n <= 0 then NULL is returned.
- If @k < 0 then NULL is returned.
- If @k > n then NULL is returned.
- S(0,0) = 1
- S(n,0) = 0
- Available in XLeratorDB / statistics 2008 only
Examples
Example #1
Let’s say that we have a fair die and we roll it 10 times. We can use the Stirling numbers of the second kind to predict the probability that the result set will contain 1, 2, 3, 4, 5 or 6 distinct values.
SELECT
k.SeriesValue as [N],
wct.BICO(6,k.seriesvalue)*
wct.STIRLING2(10,k.seriesvalue)*
wct.FACT(k.SeriesValue)*
wct.POWER(6,-10) as p
FROM
wct.Seriesint(1,6,NULL,NULL,NULL)k
This produces the following result.
Example #2
A lower triangular representation of the first few Stirling numbers of the second kind.
SELECT [1],[2],[3],[4],[5],[6],[7],[8],[9],[10]
FROM (
SELECT
n.SeriesValue as n
,k.seriesValue as k
,cast(wct.STIRLING2(n.SeriesValue,k.SeriesValue) as int) as S1
FROM
wct.SeriesInt(1,10,NULL,NULL,NULL)n
CROSS APPLY
wct.SeriesInt(1,n.seriesvalue,NULL,NULL,NULL)k
)d
PIVOT (MAX(S1) FOR k IN ([1],[2],[3],[4],[5],[6],[7],[8],[9],[10]))pvt
ORDER BY
n
This produces the following result.
See Also