History for
SWTEST - 2008
(history as of 8/7/2014 3:28:46 PM)
SWTEST
Updated: 27 June 2012
Use the aggregate function SWTEST to compute Shapiro and Wilk’s W statistic and its p-value. The p-value is the probability of observing the given result by chance.
Syntax
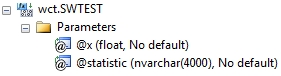
Arguments
@x
the sample values. @x is an expression of type float or of a type that can be implicitly converted to float.
@statistic
identifies the return value as either the Shapiro-Wilk statistic (w) or the p-value (p).
Return Types
float
Remarks
· If @x is null then @x is not included in the aggregate.
· @statistic must be invariant for the GROUP.
· SWTEST is an aggregate function and follows the same conventions as all other aggregate functions in SQL Server.
· @x must have at least 3 rows
Examples
In this example, we have two samples, which we have identified as sample 1 and sample 2 and we perform the Shapiro Wilk test on both in a single SELECT, grouping the results by sample number.
SELECT n.s as sample_num
,wct.SWTEST(x,'w') as w_observed
,wct.SWTEST(x,'p') as p_value
FROM (VALUES
(1,0.11),(2,3.49),
(1,7.87),(2,1.36),
(1,4.61),(2,1.14),
(1,10.14),(2,2.92),
(1,7.95),(2,2.55),
(1,3.14),(2,1.46),
(1,0.46),(2,1.06),
(1,4.43),(2,5.27),
(1,0.21),(2,-1.11),
(1,4.75),(2,3.48),
(1,0.71),(2,1.10),
(1,1.52),(2,0.88),
(1,3.24),(2,-0.51),
(1,0.93),(2,1.46),
(1,0.42),(2,0.52),
(1,4.97),(2,6.20),
(1,9.53),(2,1.69),
(1,4.55),(2,0.08),
(1,0.47),(2,3.67),
(1,6.66),(2,2.81)
) n(s,x)
GROUP BY n.s
This produces the following result
sample_num w_observed p_value
----------- ---------------------- ----------------------
1 0.900472879494979 0.0420895755448932
2 0.959026946057681 0.524597930966881
|<< Back |