OptionPLMatrix
Updated: 04 Sep 2012
Use the table-valued function OptionPLMatrix to generate a result set of profit (loss) by varying two inputs into the theoretical value of the option. For example, you could generate a result set that shows the profit (loss) based on changes in the price of the underlying asset and the volatility.
Syntax
SELECT *
FROM [wctOptions].[wct].[OptionPLMatrix] (
<@CallPut, nvarchar(4000),>
,<@AssetPrice, float,>
,<@StrikePrice, float,>
,<@TimeToMaturity, float,>
,<@RiskFreeRate, float,>
,<@DividendRate, float,>
,<@Volatility, float,>
,<@AmEur, nvarchar(4000),>
,<@Row, nvarchar(4000),>
,<@RowStep, float,>
,<@RowNumSteps, int,>
,<@Col, nvarchar(4000),>
,<@ColStep, float,>
,<@ColNumSteps, int,>)
Arguments
@CallPut
identifies the option as being a call ('C') or a put ('P'). @CallPut is an expression of type nvarchar or of a type that can be implicitly converted to nvarchar.
@AssetPrice
the price of the underlying asset. @AssetPrice is an expression of type float or of a type that can be implicitly converted to float.
@StrikePrice
the exercise price of the option. @StrikePrice is an expression of type float or of a type that can be implicitly converted to float.
@TimeToMaturity
the time to expiration of the option, expressed in years. @TimeToMaturity is an expression of type float or of a type that can be implicitly converted to float.
@RiskFreeRate
the annualized, continuously compounded risk-free rate of return over the life of the option. @RiskFreeRate is an expression of type float or of a type that can be implicitly converted to float.
@DividendRate
the annualized, continuously compounded dividend rate over the life of the option. For currency options, @DividendRate should be the foreign risk-free interest rate. @DividendRate is an expression of type float or of a type that can be implicitly converted to float.
@Volatility
the volatility of the relative price change of the underlying asset. @Volatility is an expression of type float or of a type that can be implicitly converted to float.
@AmEur
identifies the option as being American ('A') or European ('E'). @AmEur is an expression of type nvarchar or of a type that can be implicitly converted to nvarchar.
@Row
Identifies the variable which is changing with each row. @Row is an expression of type nvarchar or of a type that can be implicitly converted to nvarchar. The following values may be passed into @Row:
'S', 'U', 'ASSETP', 'UNDERLYING'
'X', 'K', 'STRIKE'
'T', 'TIME'
'R', 'RF', 'RISKFREE'
'D', 'DIV', 'DIVIDEND'
'V', 'VOL', 'VOLATILITY', 'SIGMA'
@RowStep
Identifies the value by which the intial row value is incremented and/or decremented. In the case of time ('T') the row values are only decremented and the step value is assumed to be expressed in days. @RowStep is an expression of type float or of a type that can be implicitly converted to float.
@RowNumSteps
Identifies the number of times that the initial row value is incremented and/or decremented. @RowNumSteps is an expression of type int or of a type that can be implicitly converted to int.
@Col
Identifies the variable which is changing with each column. @Col is an expression of type nvarchar or of a type that can be implicitly converted to nvarchar. The following values may be passed into @Col:
'S', 'U', 'ASSETP', 'UNDERLYING'
'X', 'K', 'STRIKE'
'T', 'TIME'
'R', 'RF', 'RISKFREE'
'D', 'DIV', 'DIVIDEND'
'V', 'VOL', 'VOLATILITY', 'SIGMA'
@ColStep
Identifies the value by which the intial column value is incremented and/or decremented. In the case of time ('T') the row values are only decremented and the step value is assumed to be expressed in days. @ColStep is an expression of type float or of a type that can be implicitly converted to float.
@ColNumSteps
Identifies the number of times that the initial column value is incremented and/or decremented. @ColNumSteps is an expression of type int or of a type that can be implicitly converted to int.
Return Types
RETURNS TABLE (
[idx_row] [int] NULL,
[idx_col] [int] NULL,
[row] [float] NULL,
[col] [float] NULL,
[val] [float] NULL
)
|
Column
|
Column Description
|
|
idx_row
|
The row index into a zero-based 2-dimensional array
|
|
idx_col
|
The column index into a zero-based 2-dimensional array
|
|
row
|
The value of the row in @Row units
|
|
col
|
The value of the column in @Col unit
|
|
val
|
The change in price, calculated using row and col
|
Remarks
· @Volatility must be greater than zero (@Volatility > 0).
· @TimeToMaturity must be greater than zero (@TimeToMaturity > 0).
· @AssetPrice must be greater than zero (@AssetPrice > 0).
· @StrikePrice must be greater than zero (@StrikePrice > 0).
· If @DividendRate is NULL an error will be returned.
· If @RiskFreeRate is NULL an error will be returned.
· @RowNumSteps must be greater than zero.
· @ColNumSteps must be greater than zero.
· European options are calculated using Black-Scholes-Merton.
· American options are calculated using Bjerksund & Stensland 2002.
· For results automatically formatted into a ‘matrix’ format, use the sp_OptionPLMatrix stored procedure.
· @Row cannot be the same as @Col.
· For matrix calculations of other option values use OptionMatrix.
Examples
In this example, we are going to calculate how the changes in the underlying and volatility will affect the profit (loss) of a Call option where the underlying is valued at 105, the strike price is 100, the option expires on 2013-06-21 and today’s date is 2012-09-04. The continuously compounded risk free rate is 2% and the continuously compounded dividend rate is 1.25%. The volatility is 20%. We have put the initial values of the option into variables simply to make the SQL easier to read.
DECLARE @s as float
DECLARE @x as float
DECLARE @t as float
DECLARE @r as float
DECLARE @d as float
DECLARE @v as float
DECLARE @z as char(1)
SET @z = 'C' --Call/Put
SET @s = 105 --Underlying
SET @x = 100 --Strike
SET @t = datediff(d,'2012-09-04','2013-06-21')/cast(365 as float) --Time
SET @r = .02 --RiskFree
SET @d = .0125 --Dividend
SET @v = .20 --Volatility
Now we will invoke the table-valued function, specifying that we want the rows to move the underlying 3 steps in increments of 0.5 and the columns to move the volatility in 2 steps in increments of 0.01. This means that we will calculate new price values where the underlying prices are 103.5, 104.0, 104.5, 105.0, 105.5, 106, and 106.5 and where the volatilities are .18, .19, .20, .21, and .22. We will then subtract out the theoretical value of the option where the underlying is 105 and the volatility is .20, which were provided as inputs to the function.
SELECT *
FROM wct.OptionPLMatrix(@z,@s,@x,@t,@r,@d,@v,'E','UNDERLYING',0.5,3,'VOL',.01,2)
This produces the following result.
idx_row idx_col row col val
----------- ----------- ---------------------- ---------------------- ----------------------
0 0 103.5 0.18 -1.64080586718804
0 1 103.5 0.19 -1.29539849756088
0 2 103.5 0.2 -0.949085002213835
0 3 103.5 0.21 -0.602018535773226
0 4 103.5 0.22 -0.254326196597994
1 0 104 0.18 -1.32613332988574
1 1 104 0.19 -0.982509081163634
1 2 104 0.2 -0.637721964048261
1 3 104 0.21 -0.291960470767997
1 4 104 0.22 0.0546190919242093
2 0 104.5 0.18 -1.00591796730666
2 1 104.5 0.19 -0.664349095992549
2 2 104.5 0.2 -0.321336407476835
2 3 104.5 0.21 0.0228933133940643
2 4 104.5 0.22 0.368152030340461
3 0 105 0.18 -0.680248061340414
3 1 105 0.19 -0.340997775599938
3 2 105 0.2 0
3 3 105 0.21 0.342477540773224
3 4 105 0.22 0.686212792724994
4 0 105.5 0.18 -0.34921483648538
4 1 105.5 0.19 -0.0125368626415181
4 2 105.5 0.2 0.326213442467953
4 3 105.5 0.21 0.666725088673203
4 4 105.5 0.22 1.00873995999709
5 0 106 0.18 -0.0129122013398231
5 1 106 0.19 0.320949601525101
5 2 106 0.2 0.657228128837545
5 3 106 0.21 0.995567131765007
5 4 106 0.22 1.33567064094265
6 0 106.5 0.18 0.328563507504093
6 1 106.5 0.19 0.659375485187226
6 2 106.5 0.2 0.992966464285587
6 3 106.5 0.21 1.32893328461522
6 4 106.5 0.22 1.66694059180434
If we were going to populate a 2-dimensional array with the calculated P&L, then Array(0,0) would contain -1.64080586718804and Array(6,4) would contain 1.66694059180434. If we are not interested in the idx_row and idx_col columns, we can explicitly select the columns that we want.
We will do that in the following example, and we will assume that we are long 100 contracts and our notional exposure is 10,000,000.
SELECT row, col, Cast(val * 10000000 as money) as val
FROM wct.OptionPLMatrix(@z,@s,@x,@t,@r,@d,@v,'E','UNDERLYING',0.5,3,'VOL',.01,2)
This produces the following result.
row col val
---------------------- ---------------------- ---------------------
103.5 0.18 -16408058.6719
103.5 0.19 -12953984.9756
103.5 0.2 -9490850.0221
103.5 0.21 -6020185.3577
103.5 0.22 -2543261.966
104 0.18 -13261333.2989
104 0.19 -9825090.8116
104 0.2 -6377219.6405
104 0.21 -2919604.7077
104 0.22 546190.9192
104.5 0.18 -10059179.6731
104.5 0.19 -6643490.9599
104.5 0.2 -3213364.0748
104.5 0.21 228933.1339
104.5 0.22 3681520.3034
105 0.18 -6802480.6134
105 0.19 -3409977.756
105 0.2 0.00
105 0.21 3424775.4077
105 0.22 6862127.9272
105.5 0.18 -3492148.3649
105.5 0.19 -125368.6264
105.5 0.2 3262134.4247
105.5 0.21 6667250.8867
105.5 0.22 10087399.60
106 0.18 -129122.0134
106 0.19 3209496.0153
106 0.2 6572281.2884
106 0.21 9955671.3177
106 0.22 13356706.4094
106.5 0.18 3285635.075
106.5 0.19 6593754.8519
106.5 0.2 9929664.6429
106.5 0.21 13289332.8462
106.5 0.22 16669405.918
If we wanted to PIVOT the results, we could enter the following SQL.
SELECT row, [0.18], [0.19], [0.20], [0.21], [0.22]
FROM (
SELECT row, col, Cast(val * 10000000 as money) as val
FROM wct.OptionPLMatrix(@z,@s,@x,@t,@r,@d,@v,'E','UNDERLYING',0.5,3,'VOL',.01,2)
) d
PIVOT (sum(val) for col in ([0.18], [0.19], [0.20], [0.21], [0.22])) as P
This produces the following result
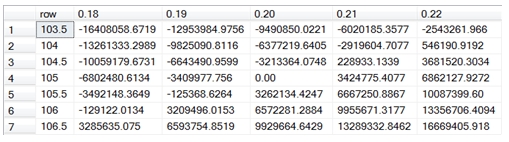
Of course, this required that we know the column-values before running the SQL. The sp_OptionPLMatrix stored procedure will automatically figure out the column headings for you and execute the SQL by call the table-valued function.
Let’s say you wanted to swap the rows and columns.
SELECT row, [103.5], [104], [104.5], [105], [105.5], [106], [106.5]
FROM (
SELECT row, col, Cast(val * 10000000 as money) as val
FROM wct.OptionPLMatrix(@z,@s,@x,@t,@r,@d,@v,'E','VOL',.01,2,'UNDERLYING',0.5,3)
) d
PIVOT (sum(val) for col in ([103.5], [104], [104.5], [105], [105.5], [106], [106.5])) as P
This produces the following result.
