MATSUB
Updated: 31 January 2012
Use the scalar function MATSUB to subtract a value from every element of a matrix or to calculate the difference between 2 matrices of the same dimensions.
MATSUB expects a string representation of the matrices, with columns separated by commas and rows separated by semi-colons.
Syntax
SELECT [wctMath].[wct].[MATSUB](
<@Matrix1, nvarchar(max),>
,<@Matrix2, nvarchar(max),>)
Arguments
@Matrix1
a string representation of a matrix.
@Matrix2
a string representation of a matrix.
Return Types
[nvarchar](max)
Remarks
· If @Matrix1 contains more than one element and @Matrix2 contains more than one element, then the number of rows and columns in @Matrix1 must be equal to the number of rows and columns in @Matrix2 or an error will be returned.
· The string representations of @Matrix1 and @Matrix2 must only contain numbers, commas (to separate the columns), and semi-colons to separate the rows.
· Consecutive commas will generate an error.
· Consecutive semi-colons will generate an error.
· Non-numeric data between commas will generate an error
· Non-number data between semi-colons will generate an error
· To convert non-normalized data to a string format, use the Matrix2String or the Matrix2String_q function.
· To convert normalized data to a string format, use the NMatrix2String or the NMatrix2String_q function.
· To convert the string result to a table, us the table-valued function MATRIX.
· To add 2 matrices, use the MATADD function.
Examples
Let’s assume that we had the following matrices, A & B, and we wanted to calculate A - B:
A = [-30,-39,64,100;-81,-62,40,-10;-66,-59,-99,-57;34,37,5,22;40,9,68,-5]
B = [20,41,-46,2;-47,0,54,41;38,-70,-16,95;4,77,70,-81;47,-41,-55,-46]
We could enter the following SQL to perform the addition.
DECLARE @A as varchar(max)
DECLARE @B as varchar(max)
SET @A = '-30,-39,64,100;-81,-62,40,-10;-66,-59,-99,-57;34,37,5,22;40,9,68,-5'
SET @B = '20,41,-46,2;-47,0,54,41;38,-70,-16,95;4,77,70,-81;47,-41,-55,-46'
SELECT wct.MATSUB(@A, @B) as [A-B]
This produces the following result.
A-B
---------------------------------------------------------------------------
-50,-80,110,98;-34,-62,-14,-51;-104,11,-83,-152;30,-40,-65,103;-7,50,123,41
Because this subtraction, order matters, so if we switch the matrices in the function, we will get a different result.
SELECT wct.MATSUB(@B, @A) as [B-A]
This produces the following result.
B-A
----------------------------------------------------------------------- 50,80,-110,-98;34,62,14,51;104,-11,83,152;-30,40,65,-103;7,-50,-123,-41
The matrices do not have to assigned variables before passed into the MATSUB function; the strings can be passed in directly.
SELECT wct.MATSUB('-30,-39,64,100;-81,-62,40,-10;-66,-59,-99,-57;34,37,5,22;40,9,68,-5', '20,41,-46,2;-47,0,54,41;38,-70,-16,95;4,77,70,-81;47,-41,-55,-46') as [A-B]
This produces the following result.
A-B
---------------------------------------------------------------------------
-50,-80,110,98;-34,-62,-14,-51;-104,11,-83,-152;30,-40,-65,103;-7,50,123,41
In this example, we are going to subtract 5 from every element in the @A matrix.
DECLARE @A as varchar(max)
DECLARE @B as varchar(max)
SET @A = '-30,-39,64,100;-81,-62,40,-10;-66,-59,-99,-57;34,37,5,22;40,9,68,-5'
SET @B = '5'
SELECT wct.MATSUB(@A, @B) as [A-B]
This produces the following result.
A-B
--------------------------------------------------------------------
-35,-44,59,95;-86,-67,35,-15;-71,-64,-104,-62;29,32,0,17;35,4,63,-10
If we switched the order of the matrices we get a different result.
SELECT wct.MATSUB(@B, @A) as [B-A]
This produces the following result.
B-A
-------------------------------------------------------------------
35,44,-59,-95;86,67,-35,15;71,64,104,62;-29,-32,0,-17;-35,-4,-63,10
In this example, the matrix values are stored on a table in the database and are converted to a string value using the MATRIX2STRING function.
/* Put A into a table */
SELECT *
INTO #A
FROM (
SELECT -30,-39,64,100 UNION ALL
SELECT -81,-62,40,-10 UNION ALL
SELECT -66,-59,-99,-57 UNION ALL
SELECT 34,37,5,22 UNION ALL
SELECT 40,9,68,-5
) A(xo,x1,x2,x3)
/* Put B into a table */
SELECT *
INTO #B
FROM (
SELECT 20,41,-46,2 UNION ALL
SELECT -47,0,54,41 UNION ALL
SELECT 38,-70,-16,95 UNION ALL
SELECT 4,77,70,-81 UNION ALL
SELECT 47,-41,-55,-46
) B(x0,x1,x2,x3)
/* Do the matrix subtraction */
SELECT wct.MATSUB(wct.MATRIX2STRING('#A','*','',NULL), wct.MATRIX2STRING('#B','*','',NULL)) as [A-B]
This produces the following result.
A-B
---------------------------------------------------------------------------
-50,-80,110,98;-34,-62,-14,-51;-104,11,-83,-152;30,-40,-65,103;-7,50,123,41
If we wanted to return the matrix sum as a normalized table, we can use the table-valued function MATRIX to do that.
SELECT *
FROM wct.MATRIX((SELECT wct.MATSUB('-30,-39,64,100;-81,-62,40,-10;-66,-59,-99,-57;34,37,5,22;40,9,68,-5','20,41,-46,2;-47,0,54,41;38,-70,-16,95;4,77,70,-81;47,-41,-55,-46')))
This produces the following result.
RowNum ColNum ItemValue
----------- ----------- ----------------------
0 0 -50
0 1 -80
0 2 110
0 3 98
1 0 -34
1 1 -62
1 2 -14
1 3 -51
2 0 -104
2 1 11
2 2 -83
2 3 -152
3 0 30
3 1 -40
3 2 -65
3 3 103
4 0 -7
4 1 50
4 2 123
4 3 41
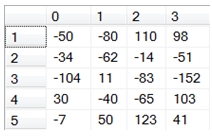
If we wanted to return the results in matrix form, we can use the PIVOT function, though this requires knowing the number of columns returned by the function (which is the number of columns in the second array).
SELECT [0],[1],[2],[3]
FROM (
SELECT *
FROM wct.MATRIX((SELECT wct.MATSUB('-30,-39,64,100;-81,-62,40,-10;-66,-59,-99,-57;34,37,5,22;40,9,68,-5','20,41,-46,2;-47,0,54,41;38,-70,-16,95;4,77,70,-81;47,-41,-55,-46')))
) M PIVOT(
MAX(ItemValue)
FOR colnum IN([0],[1],[2],[3])
) AS pvt
ORDER BY rownum
This produces the following result.