CORRM
Updated: 05 March 2015
Use the table-valued function CORRM to calculate a correlation matrix. Given a matrix Am,n and a covariance matrix Cn,n = COVM (Am,n), then each element in correlation matrix Rn,n is calculated as:
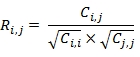
For example:

Syntax
SELECT * FROM [wct].[CORRM](
<@Matrix_RangeQuery, nvarchar(max),>
,<@Is3N, bit,>)
Arguments
@Matrix_RangeQuery
the SELECT statement, as text, used to return the input matrix for this function. The SELECT statement specifies the column names from the table or view or can be used to enter the matrix values directly. Data returned from the @Matrix_RangeQuery select must be of the type float or of a type that implicitly converts to float.
@Is3N
a bit value identifying the form for the resultant table returned by @Matrix_RangeQuery. Enter 'True' for a resultant table in 3rd normal form. Enter 'False' for a de-normalized table in 'spreadsheet' form.
Return Types
TABLE (
[RowNum] [int] NULL,
[ColNum] [int] NULL,
[ItemValue] [float] NULL
Remarks
· If @Is3N is NULL then @Is3N = 'False'.
· Use MCORR for a matrix stored as a string.
· If @Is3N is'True' then the result table should be returned as row, column, and value.
· If the array contains NULL, then NULL will be returned.
· The function returns an error if the array contains a non-numeric value.
· If the supplied input is a vector, then result will be the (sample) variance.
Examples
In this example @Matrix_RangeQuery returns the matrix from a derived table embodied in the statement. The matrix is in spreadsheet form.
SELECT
*
FROM
wct.CORRM(
'SELECT
x1,x2,x3,x4,x5,x6,x7,x8
FROM (VALUES
(1,1,1,1,1,1,1,1)
,(2,3,4,5,6,7,8,9)
,(4,9,16,25,36,49,64,81)
)n(x1,x2,x3,x4,x5,x6,x7,x8)'
,'False'
)
This produces the following result.
Note that the results are returned in third-normal form. If we wanted to a more traditional (de-normalized) presentation of the results, we can us the PIVOT function. Also note that we can use * to select all the columns. We have rounded the results to 4 decimal place for ease of viewing.
SELECT
ROUND([0],4) as [0],
ROUND([1],4) as [1],
ROUND([2],4) as [2],
ROUND([3],4) as [3],
ROUND([4],4) as [4],
ROUND([5],4) as [5],
ROUND([6],4) as [6],
ROUND([7],4) as [7]
FROM (
SELECT
*
FROM
wct.CORRM(
'SELECT
*
FROM (VALUES
(1,1,1,1,1,1,1,1)
,(2,3,4,5,6,7,8,9)
,(4,9,16,25,36,49,64,81)
)n(x1,x2,x3,x4,x5,x6,x7,x8)'
,'False'
)
) d
PIVOT(SUM(ItemValue) for ColNum in([0],[1],[2],[3],[4],[5],[6],[7])) as P
This produces the following result.
Let's put several matrices into a table and calculate the correlation matrix for each. We will use CROSS APPLY to calculate to the correlation matrix for each matrix. Note that we have to convert the matrix identifier (which is defined as int) to a varchar to include it in the WHERE clause of @Matrix_RangeQuery.
CREATE TABLE #c(
Matrix int,
rn int,
x1 float,
x2 float,
x3 float,
PRIMARY KEY (Matrix, rn)
)
INSERT INTO #c VALUES (100,1,-11,-41,36)
INSERT INTO #c VALUES (100,2,-31,41,-47)
INSERT INTO #c VALUES (100,3,48,-38,33)
INSERT INTO #c VALUES (100,4,8,44,-10)
INSERT INTO #c VALUES (101,1,39,6,-7)
INSERT INTO #c VALUES (101,2,33,-49,16)
INSERT INTO #c VALUES (101,3,14,29,13)
INSERT INTO #c VALUES (101,4,35,-38,-50)
INSERT INTO #c VALUES (101,5,9,-32,-25)
INSERT INTO #c VALUES (102,1,29,49,-17)
INSERT INTO #c VALUES (102,2,35,28,28)
INSERT INTO #c VALUES (102,3,-34,-29,-49)
INSERT INTO #c VALUES (102,4,0,-5,0)
INSERT INTO #c VALUES (102,5,-17,14,24)
INSERT INTO #c VALUES (102,6,44,3,-23)
SELECT
n.MATRIX
,k.*
FROM
(SELECT DISTINCT MATRIX FROM #c)n
CROSS APPLY
wct.CORRM(
'SELECT
x1,x2,x3
FROM
#c
WHERE MATRIX = ' + cast(n.Matrix as varchar(max)) + ' ORDER by rn'
,'False'
)k
This produces the following result.
In this example we calculate the correlation matrix from a derived table in 3rd normal form.
SELECT
*
FROM
wct.CORRM(
'SELECT
rownum,colnum,itemvalue
FROM (VALUES
(0,0,1),(0,1,1),(0,2,1),(0,3,1),(0,4,1),(0,5,1),(0,6,1),(0,7,1)
,(1,0,2),(1,1,3),(1,2,4),(1,3,5),(1,4,6),(1,5,7),(1,6,8),(1,7,9)
,(2,0,4),(2,1,9),(2,2,16),(2,3,25),(2,4,36),(2,5,49),(2,6,64),(2,7,81)
)n(rownum,colnum,itemvalue)'
,'True'
)
This produces the following result.
See Also