PRICEACT
Updated: 31 October 2014
Use the scalar function PRICEACT to calculate the price from yield of a bond where the coupon amounts are calculated as the actual number of days in the coupon period divided by the number of days in the year. This means that the coupon amounts will vary from period. The number of days in the year is either 360, 365, or 366 based upon the day-count convention. PRICEACT also allows the entry of a forced redemption schedule.
The price of the bond is the discounted cash flow value of all the remaining payments minus the accrued interest.
The formula for the price of a bond with more than one coupon period to redemption using the actual number of days in each coupon period is:
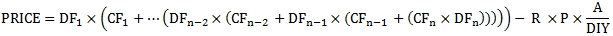
Where:
|
A
|
=
|
Actual number of days from the previous coupon date to the settlement date
|
|
CFn
|
=
|
Cash Flow for period n
|
|
DFn
|
=
|
Discount factor for period n
|
|
DIY
|
=
|
Number of days in the year in which the coupon payment occurs
|
|
n
|
=
|
Number of coupons from settlement date to maturity date
|
|
P
|
=
|
Par value of the security
|
|
R
|
=
|
Coupon rate
|
and
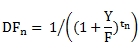
Where
|
F
|
=
|
The number of coupon payments per year
|
|
t1
|
=
|
Time, in years, from the settlement date to the first coupon date
|
|
tn
|
=
|
Time, in years, of the coupon period
|
|
Y
|
=
|
Annual yield
|
and
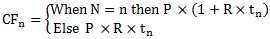
Where
|
P
|
=
|
Par value of the security
|
|
R
|
=
|
Coupon rate
|
|
tn
|
=
|
Time, in years, of the coupon period
|
In the case where there are forced redemptions (i.e. partial repayments of principal prior to the maturity date of security), then the formula needs to be adjusted to reflect those redemptions in the cash flows (CFn) and the price calculation then becomes:

Where P/Prin is the par value divided by the outstanding principal balance as of the coupon date immediately prior to the settlement date.
In the case where the settlement date is in the final coupon then the formula for the price of the bond is the same as the formula used in PRICE function.
Syntax
SELECT [wct].[PRICEACT](
<@Settlement, datetime,>
,<@Maturity, datetime,>
,<@Rate, float,>
,<@Par, float,>
,<@Yield, float,>
,<@Frequency, float,>
,<@Basis, nvarchar(4000),>
,<@Repayments, nvarchar(max),>)
Arguments
@Settlement
the settlement date of the security. @Settlement is an expression that returns a datetime or smalldatetime value, or a character string in date format.
@Maturity
the maturity date of the security. @Maturity is an expression that returns a datetime or smalldatetime value, or a character string in date format.
@Rate
the security’s annual coupon rate. @Rate is an expression of type float or of a type that can be implicitly converted to float.
@Par
the par value of the security. Any forced redemptions are subtracted from the par value on the redemption date and the adjusted balance is used in calculating the subsequent coupon interest. @Par is an expression of type float or of a type that can be implicitly converted to float.
@Yield
the security’s annual yield. @Yield is an expression of type float or of a type that can be implicitly converted to float.
@Frequency
the number of coupon payments per year. For annual payments, @Frequency = 1; for semi-annual, @Frequency = 2; for quarterly, @Frequency = 4; for bi-monthly, @Frequency = 6, for monthly, @Frequency = 12. @Frequency is an expression of type float or of a type that can be implicitly converted to float.
@Basis
is the type of day count to use. @Basis is an expression of the character string data type category.
|
@Basis
|
Day count basis
|
|
1, 'ACTUAL'
|
Actual/Actual
|
|
2, 'A360'
|
Actual/360
|
|
3, 'A365'
|
Actual/365
|
|
11, 'ACTUAL NON-EOM'
|
Actual/Actual non-end-of-month
|
|
12, 'A360 NON-EOM'
|
Actual/360 non-end-of-month
|
|
13, 'A365 NON-EOM'
|
Actual/365 non-end-of-month
|
@Repayments
a SELECT statement, as a string, which identifies the coupon dates and the forced redemption amounts to be used in the price calculation.
Return Type
float
Remarks
· If @Basis is invalid then PRICEACT returns an error.
· If @Frequency is invalid then PRICEACT returns an error.
· If @Maturity < @Settlement then NULL is returned.
· If @Repayments returns NULL then @Par is used for all interest calculations and as the redemption value.
· If @Settlement is NULL, @Settlement = GETDATE().
· If @Frequency is NULL, @Frequency = 2.
· If @Basis is NULL, @Basis = 1.
· PRICEACT forces the principal balance of the bond to zero at maturity.
· If @Par is NULL then @Par = 100.
· If @Rate is NULL then @Rate = 0.
· If @Yield is NULL then @Yield = 0.
· If @Maturity is NULL then PRICEACT returns NULL.
· If @Basis = 3 or @Basis = 13 then the number of days in a year is always 365.
· If @Basis =2 or @Basis = 12 then the number of days in a year is always 360.
· If @Basis =1 or @Basis = 1 then the number of days in a year is determined by the actual number of days in the year of coupon period end date.
Examples
In this example we calculate the price of a bond maturity on 2034-11-01 with a coupon interest rate of 11.0% paying interest semi-annually. The bond is priced at a yield of 12.5% and is settling on 2014-10-29. The bond uses the actual/actual day-count convention.
SELECT
wct.PRICEACT(
'2014-10-29' --@Settlement
,'2034-11-01' --@Maturity
,0.11 --@Rate
,100 --@Par
,0.125 --@Yield
,2 --@Frequency
,1 --@Basis
,NULL --@Repayments
) as PRICE
This produces the following result.
PRICE
----------------------
89.0583463371609
Let's compare this to the result returned by the PRICE function.
SELECT
wct.PRICEACT(
'2014-10-29' --@Settlement
,'2034-11-01' --@Maturity
,0.11 --@Rate
,100 --@Par
,0.125 --@Yield
,2 --@Frequency
,1 --@Basis
,NULL --@Repayments
) as PRICEACT
,wct.PRICE(
'2014-10-29' --@Settlement
,'2034-11-01' --@Maturity
,0.11 --@Rate
,0.125 --@Yield
,100 --@Redemption
,2 --@Frequency
,1 --@Basis
) as PRICE
This produces the following result.
PRICEACT PRICE
---------------------- ----------------------
89.0583463371609 89.0580044972901
In this example we have a bond maturing on 2019-10-31 with a 12.5% coupon paid semi-annually. The bond has 16 equal forced redemptions starting with the 2012-04-30 coupon. The bond is priced at a yield of 12.5% settling on 2014-10-29.
SELECT
wct.PRICEACT(
'2014-10-29' --@Settlement
,'2019-10-31' --@Maturity
,0.125 --@Rate
,100 --@Par
,0.125 --@Yield
,2 --@Frequency
,1 --@Basis
,'SELECT
*
FROM (VALUES
(''2012-04-30'',6.25)
,(''2012-10-31'',6.25)
,(''2013-04-30'',6.25)
,(''2013-10-31'',6.25)
,(''2014-04-30'',6.25)
,(''2014-10-31'',6.25)
,(''2015-04-30'',6.25)
,(''2015-10-31'',6.25)
,(''2016-04-30'',6.25)
,(''2016-10-31'',6.25)
,(''2017-04-30'',6.25)
,(''2017-10-31'',6.25)
,(''2018-04-30'',6.25)
,(''2018-10-31'',6.25)
,(''2019-04-30'',6.25)
,(''2019-10-31'',6.25)
)n(dt_ppay, amt_ppay)' --@Repayments
) as PRICE
This produces the following result.
PRICE
----------------------
99.9985011972914
See Also