IAM
Updated: 10 October 2014
Use IAM to calculate the price or yield for a bond that pays interest at maturity and has a par value of 100. The formula for price is:
Where:
|
A
|
=
|
Number of days from issue date to settlement date
|
|
B
|
=
|
Number of days in the year
|
|
DIM
|
=
|
Number of days from issue date to maturity date
|
|
DSM
|
=
|
Number of days from settlement date to maturity date
|
|
P
|
=
|
Price per 100 par value
|
|
R
|
=
|
Annual interest rate in decimal terms
|
|
Y
|
=
|
Annual Yield
|
The formula for yield is:
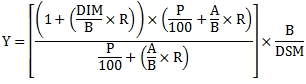
Where:
|
A
|
=
|
Number of days from issue date to settlement date
|
|
B
|
=
|
Number of days in the year
|
|
DIM
|
=
|
Number of days from issue date to maturity date
|
|
DSM
|
=
|
Number of days from settlement date to maturity date
|
|
P
|
=
|
Price per 100 par value
|
|
R
|
=
|
Annual interest rate in decimal terms
|
|
Y
|
=
|
Annual Yield
|
The IAM function allows you to pass values for A, B, DIM, DSM, and R directly into the function and automatically calculates Y and P.
Syntax
SELECT [wctFinancial].[wct].[IAM](
<@A, float,>
,<@B, float,>
,<@D_IM, float,>
,<@DSM, float,>
,<@R, float,>
,<@P, float,>
,<@Y, float,>)
Arguments
@A
the number of days from issue to settlement. @A is an expression of type float or of a type that can be implicitly converted to float.
@B
the number days in the year. @DSC is an expression of type float or of a type that can be implicitly converted to float.
@D_IM
the number of days from issue to maturity. @D_IM is an expression of type float or of a type that can be implicitly converted to float.
@DSM
the number of days from settlement to maturity. @DSM is an expression of type float or of a type that can be implicitly converted to float.
@R
the annual interest rate. @R is an expression of type float or of a type that can be implicitly converted to float.
@P
the price of the security. @P is an expression of type float or of a type that can be implicitly converted to float.
@Y
the yield on the security. @Y is an expression of type float or of a type that can be implicitly converted to float.
Return Type
float
Remarks
· If @A is NULL then @A = @D_IM - @DSM.
· If @B is NULL then @B =360.
· If @D_IM is NULL then @D_IM = 0.
· If @DSM is NULL then @DSM = 0.
· If @R is NULL then @R = 0.
· If @Y is NULL and @P is NULL then NULL is returned.
· If @Y is not NULL then the function calculates the price from the inputs otherwise the function calculates the yield.
Examples
In this example we calculate the price for a security with an interest rate of 0.5%. There are 68 accrued days, 137 days from issue to maturity, 69 days from settlement to maturity, and 365 days in the year. The yield is 0.2%
SELECT
wct.IAM(
68 --@A
,365 --@B
,137 --@D_IM
,69 --@DSM
,0.005 --@R
,NULL --@P
,0.002 --@Y
) as Price
This produce the following result.
Price
----------------------
100.056655689645
In this example we calculate the yield for a security with an interest rate -0.05%. There are 108 days from issue to maturity, 55 days from settlement to maturity, and 360 days in the year. The price is 99.977088.
SELECT
wct.IAM(
NULL --@A
,360 --@B
,108 --@D_IM
,55 --@DSM
,-0.0005 --@R
,99.977088 --@P
,NULL --@Y
) as Yield
This produces the following result.
Yield
----------------------
0.000999997275740647
In this example we calculate the price for a security with an interest rate of 0.2%. The yield is -0.05%. There are 95 days from issue to maturity, 38 days from settlement to maturity, and 360 days in the year.
SELECT
wct.IAM(
NULL --@A
,360 --@B
,95 --@D_IM
,38 --@DSM
,0.002 --@R
,NULL --@P
,-0.0005 --@Y
) as Price
This produces the following result.
Price
----------------------
100.026391953094
In this example we calculate the yield for a security with an interest rate 0.07%. There are 181 days from issue to maturity, 83 days from settlement to maturity, and 364 days in the year. The price is 99.628637.
SELECT
wct.IAM(
NULL --@A
,364 --@B
,181 --@D_IM
,83 --@DSM
,0.07 --@R
,99.628637 --@P
,NULL --@Y
) as Yield
This produces the following result.
Yield
----------------------
0.0850000161919074
See Also