PRICEFR
Updated: 17 October 2014
Use the scalar function PRICEFR to calculate the price from yield of a bond with a forced redemption schedule where the coupon payment dates occur at regular periods and the redemptions can occur on any coupon date. The formula for the price of a bond with a forced redemption schedule with more than one period to maturity is:
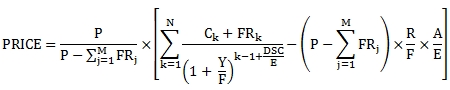
Where:
|
A
|
=
|
Number of days from previous coupon date to settlement date
|
|
C
|
=
|
Coupon Amount
|
|
DSC
|
=
|
Number of days from settlement date to the next coupon date
|
|
E
|
=
|
Number of days in the current coupon period
|
|
F
|
=
|
Number of coupon payments per year
|
|
FR
|
=
|
Forced Redemption amount
|
|
M
|
=
|
Number of forced redemptions on or before the previous coupon date
|
|
N
|
=
|
Number of coupons from the settlement to the maturity date
|
|
P
|
=
|
Par Value
|
|
R
|
=
|
Annual interest rate in decimal terms (10% = 0.10)
|
|
Y
|
=
|
Annual yield in decimal terms (10% = 0.10)
|
The coupon payments can vary over the life of the bond as they are affected by the forced redemption schedule. Coupon payments are calculated as
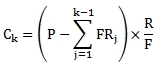
Where:
|
Ck
|
=
|
Coupon payment number k
|
|
F
|
=
|
Number of coupon payments per year
|
|
FR
|
=
|
Forced redemption amount
|
|
P
|
=
|
Par value
|
|
R
|
=
|
Annual rate of interest in decimal terms
|
If the settlement date is in the final coupon period, then the formula for the calculation of price is:
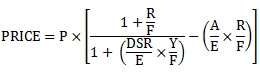
Where:
|
A
|
=
|
Number of days from previous coupon date to settlement date
|
|
DSR
|
=
|
Number of days from settlement date to maturity date
|
|
E
|
=
|
Number of days in the current coupon period
|
|
F
|
=
|
Number of coupon payments per year
|
|
R
|
=
|
Annual interest rate in decimal terms (10% = 0.10)
|
|
P
|
=
|
Par Value
|
|
Y
|
=
|
Annual yield in decimal terms (10% = 0.10)
|
Syntax
SELECT [wct].[PRICEFR](
<@Settlement, datetime,>
,<@Maturity, datetime,>
,<@Rate, float,>
,<@Par, float,>
,<@Yield, float,>
,<@Frequency, float,>
,<@Basis, nvarchar(4000),>
,<@Repayments, nvarchar(max),>)
Arguments
@Settlement
the settlement date of the security. @Settlement is an expression that returns a datetime or smalldatetime value, or a character string in date format.
@Maturity
the maturity date of the security. @Maturity is an expression that returns a datetime or smalldatetime value, or a character string in date format.
@Rate
the security’s annual coupon rate. @Rate is an expression of type float or of a type that can be implicitly converted to float.
@Par
the par value of the security. All forced redemptions are subtracted from the par value on the redemption date and the adjusted balance is used in calculating the subsequent coupon interest. @Par is an expression of type float or of a type that can be implicitly converted to float.
@Yield
the security’s annual yield. @Yield is an expression of type float or of a type that can be implicitly converted to float.
@Frequency
the number of coupon payments per year. For annual payments, @Frequency = 1; for semi-annual, @Frequency = 2; for quarterly, @Frequency = 4; for bimonthly @Frequency = 6; for monthly, @Frequency = 12. For bonds with @Basis = 'A/364' or 9, you can enter 364 for payments made every 52 weeks, 182 for payments made every 26 weeks, 91 for payments made every 13 weeks, 28 for payments made every 4 weeks, 14 for payments made every 2 weeks, and 7 for weekly payments. @Frequency is an expression of type float or of a type that can be implicitly converted to float.
@Basis
is the type of day count to use. @Basis is an expression of the character string data type category.
|
@Basis
|
Day count basis
|
|
0, 'BOND'
|
US (NASD) 30/360
|
|
1, 'ACTUAL'
|
Actual/Actual
|
|
2, 'A360'
|
Actual/360
|
|
3, 'A365'
|
Actual/365
|
|
4, '30E/360 (ISDA)', '30E/360', 'ISDA', '30E/360 ISDA', 'EBOND'
|
European 30/360
|
|
5, '30/360', '30/360 ISDA', 'GERMAN'
|
30/360 ISDA
|
|
6, 'NL/ACT'
|
No Leap Year/ACT
|
|
7, 'NL/365'
|
No Leap Year /365
|
|
8, 'NL/360'
|
No Leap Year /360
|
|
9, 'A/364'
|
Actual/364
|
|
10, 'BOND NON-EOM'
|
US (NASD) 30/360 non-end-of-month
|
|
11, 'ACTUAL NON-EOM'
|
Actual/Actual non-end-of-month
|
|
12, 'A360 NON-EOM'
|
Actual/360 non-end-of-month
|
|
13, 'A365 NON-EOM'
|
Actual/365 non-end-of-month
|
|
14, '30E/360 NON-EOM', '30E/360 ICMA NON-EOM', 'EBOND NON-EOM'
|
European 30/360 non-end-of-month
|
|
15, '30/360 NON-EOM', '30/360 ISDA NON-EOM', 'GERMAN NON-EOM'
|
30/360 ISDA non-end-of-month
|
|
16, 'NL/ACT NON-EOM'
|
No Leap Year/ACT non-end-of-month
|
|
17, 'NL/365 NON-EOM'
|
No Leap Year/365 non-end-of-month
|
|
18, 'NL/360 NON-EOM'
|
No Leap Year/360 non-end-of-month
|
|
19, 'A/364 NON-EOM'
|
Actual/364 non-end-of-month
|
@Repayments
a SELECT statement, as a string, which identifies the coupon dates and the forced redemption amounts to be used in the price calculation.
Return Type
float
Remarks
· If @Basis is invalid then PRICEFR returns an error.
· If @Frequency is invalid then PRICEFR returns an error.
· If @Maturity < @Settlement then NULL is returned.
· If @Repayments returns no rows then NULL is returned.
· If @Settlement is NULL, @Settlement = GETDATE().
· If @Frequency is NULL, @Frequency = 2.
· If @Basis is NULL, @Basis = 0.
· PRICEFR forces the principal balance of the bond to zero at maturity.
· If @Par is NULL then @Par = 100.
· If @Rate is NULL then @Rate = 0.
· If @Yield is NULL then @Yield = 0.
· If @Maturity is NULL then PRICEFR returns NULL.
Example
In this example we calculate the price of a bond maturing on 2029-09-15 with the following redemption schedule:
2017-09-25 28.074
2021-09-20 32.29189696
2024-09-15 39.63410304
The bond has an 11.0% coupon rate, pays interest every 182 days using the Actual/364 day-count convention and has a par value or 100. The bond is being purchased at a yield of 10.75% for settlement on 2014-10-16.
SELECT
wct.PRICEFR(
'2014-10-16' --@Settlement
,'2025-09-15' --@Maturity
,0.1100 --@Rate
,100 --@Par
,0.1075 --@Yield
,182 --@Frequency
,9 --@Basis
,'SELECT
*
FROM (VALUES
(''2017,09,25'', 28.074),
(''2021,09,20'', 32.29189696),
(''2025,09,15'', 39.63410304)
)n(date_cf, amt_cf)' --@Repayments
) as [PRICE]
This produces the following result.
PRICE
----------------------
101.178910626482
In this example, we eliminate the last row in the @Repayments SQL, demonstrating that PRICEFR will always force the principal amount at maturity equal to zero.
SELECT
wct.PRICEFR(
'2014-10-16' --@Settlement
,'2025-09-15' --@Maturity
,0.1100 --@Rate
,100 --@Par
,0.1075 --@Yield
,182 --@Frequency
,9 --@Basis
,'SELECT
*
FROM (VALUES
(''2017,09,25'', 28.074),
(''2021,09,20'', 32.29189696)
)n(date_cf, amt_cf)' --@Repayments
) as [PRICE]
This produces the following result.
PRICE
----------------------
101.178910626482
In this example, we populate a table with forced redemption information for a number of securities and demonstrate how to select that data in the @Repayments SQL.
SELECT
*
INTO
#Repayments
FROM (VALUES
('KE1000001637','16-Feb-15',43.00)
,('KE1000001637','13-Feb-17',22.80)
,('KE1000001637','8-Feb-21',34.20)
,('KE1000001758','30-Nov-2015',48.648)
,('KE1000001758','26-Nov-2018',27.23299264)
,('KE1000001758','22-Nov-2021',24.11900736)
,('KE1000001793','22-Feb-2016',55.17)
,('KE1000001793','19-Feb-2018',44.83)
,('KE1000001954','22-Aug-2016',43.038)
,('KE1000001954','21-Aug-2017',26.53232998)
,('KE1000001954','19-Aug-2019',30.42967002)
,('KE2000002242','28-Sep-2015',44.01)
,('KE2000002242','23-Sep-2019',32.6634462)
,('KE2000002242','18-Sep-2023',23.3265538)
,('KE3000008130','25-Sep-2017',28.074)
,('KE3000008130','20-Sep-2021',32.29189696)
,('KE3000008130','15-Sep-2025',39.63410304)
)n(ISIN, dt_ppay, amt_ppay)
SELECT
wct.PRICEFR(
'2014-10-16' --@Settlement
,'2025-09-15' --@Maturity
,0.1100 --@Rate
,100 --@Par
,0.1075 --@Yield
,182 --@Frequency
,9 --@Basis
,'SELECT
dt_ppay
,amt_ppay
FROM
#Repayments
WHERE
ISIN = ''' + 'KE3000008130' + '''' --@Repayments
) as [PRICE]
This produces the following result.
PRICE
----------------------
101.178910626482
In this example we calculate the price for multiple securities, all with the same settlement date and yield, pulling the forced redemptions in from a temp table and the rest of the function inputs from a derived table.
SELECT
*
INTO
#Repayments
FROM (VALUES
('KE1000001637','16-Feb-15',43.00)
,('KE1000001637','13-Feb-17',22.80)
,('KE1000001637','8-Feb-21',34.20)
,('KE1000001758','30-Nov-2015',48.648)
,('KE1000001758','26-Nov-2018',27.23299264)
,('KE1000001758','22-Nov-2021',24.11900736)
,('KE1000001793','22-Feb-2016',55.17)
,('KE1000001793','19-Feb-2018',44.83)
,('KE1000001954','22-Aug-2016',43.038)
,('KE1000001954','21-Aug-2017',26.53232998)
,('KE1000001954','19-Aug-2019',30.42967002)
,('KE2000002242','28-Sep-2015',44.01)
,('KE2000002242','23-Sep-2019',32.6634462)
,('KE2000002242','18-Sep-2023',23.3265538)
,('KE3000008130','25-Sep-2017',28.074)
,('KE3000008130','20-Sep-2021',32.29189696)
,('KE3000008130','15-Sep-2025',39.63410304)
)n(ISIN, dt_ppay, amt_ppay)
SELECT
n.ISIN
,wct.PRICEFR(
'2014-10-16' --@Settlement
,n.Maturity --@Maturity
,n.Rate --@Rate
,100 --@Par
,0.1075 --@Yield
,n.Frequency --@Frequency
,n.Basis --@Basis
,'SELECT
dt_ppay
,amt_ppay
FROM
#Repayments
WHERE
ISIN = ''' + cast(n.ISIN as varchar(max)) + '''' --@Repayments
) as [PRICE]
FROM (VALUES
('KE1000001637','2021-02-08',0.125,182,9)
,('KE1000001758','2021-11-22',0.120,182,9)
,('KE1000001793','2018-02-19',0.120,182,9)
,('KE1000001954','2019-08-19',0.060,182,9)
,('KE2000002242','2023-09-19',0.120,182,9)
,('KE3000008130','2025-09-15',0.110,182,9)
)n(ISIN,Maturity,Rate,Frequency,Basis)
This produces the following result.
ISIN PRICE
------------ ----------------------
KE1000001637 103.713940670862
KE1000001758 103.185247973971
KE1000001793 102.362895728426
KE1000001954 88.2317399662709
KE2000002242 103.235732864288
KE3000008130 101.178910626482
In this example we calculate the price of the bond after a redemption has occurred.
SELECT
wct.PRICEFR(
'2017-10-01' --@Settlement
,'2025-09-15' --@Maturity
,0.1100 --@Rate
,100 --@Par
,0.1075 --@Yield
,182 --@Frequency
,9 --@Basis
,'SELECT
*
FROM (VALUES
(''2017,09,25', 28.074),
(''2021,09,20', 32.29189696)
)n(date_cf, amt_cf)' --@Repayments
) as [PRICE]
This produces the following result.
PRICE
----------------------
101.077556509014
In this example. we calculate the price of the bond in the final coupon period.
SELECT
wct.PRICEFR(
'2025-08-15' --@Settlement
,'2025-09-15' --@Maturity
,0.1100 --@Rate
,100 --@Par
,0.1075 --@Yield
,182 --@Frequency
,9 --@Basis
,'SELECT
*
FROM (VALUES
(''2017,09,25', 28.074),
(''2021,09,20', 32.29189696)
)n(date_cf, amt_cf)' --@Repayments
) as [PRICE]
This produces the following result.
PRICE
----------------------
99.9797000808397
This is an example of a bond paying a coupon semi-annually using the Actual/Actual day-count convention.
SELECT
wct.PRICEFR(
'2014-10-16' --@Settlement
,'2034-11-01' --@Maturity
,0.0475 --@Rate
,100 --@Par
,0.0400 --@Yield
,2 --@Frequency
,1 --@Basis
,'SELECT
*
FROM (VALUES
(''2026,11,01', 20.000),
(''2028,11,01', 20.000),
(''2030,11,01', 20.000),
(''2032,11,01', 20.000)
)n(date_cf, amt_cf)' --@Repayments
) as [PRICE]
This produces the following result.
PRICE
----------------------
108.753442328922
See Also