PRICE
Updated: 05 May 2014
Use PRICE to calculate the price for a security that pays periodic interest and has a par value of 100. The formula for price with more than one coupon period to redemption is:
Where
C = 100 * coupon rate / frequency
Y = yield / frequency
RV = redemption value
DSC = number of days from settlement to coupon
N = the number of coupons between the settlement date and the maturity date
E = the number of days in the current coupon period
A = C * accrued days / E
When the settlement date is greater than or equal to the last coupon date, the formula for price is:
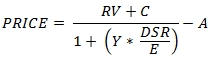
Where
C = 100 * coupon rate / frequency
Y = yield / frequency
RV = redemption value
DSR = number of days from settlement to redemption
E = the number of days in the current coupon period
A = C * accrued days / E
Syntax
SELECT [westclintech].[wct].[PRICE] (
<@Settlement, datetime,>
,<@Maturity, datetime,>
,<@Rate, float,>
,<@Yld, float,>
,<@Redemption, float,>
,<@Frequency, float,>
,<@Basis, nvarchar(4000),>)
Arguments
@Settlement
the settlement date of the security. @Settlement is an expression that returns a datetime or smalldatetime value, or a character string in date format.
@Maturity
the maturity date of the security. @Maturity is an expression that returns a datetime or smalldatetime value, or a character string in date format.
@Rate
the security’s annual coupon rate. @Rate is an expression of type float or of a type that can be implicitly converted to float.
@Yld
the security’s annual yield. @Yld is an expression of type float or of a type that can be implicitly converted to float.
@Redemption
the security’s redemption value per 100 face value. @Redemption is an expression of type float or of a type that can be implicitly converted to float.
@Frequency
the number of coupon payments per year. For annual payments, @Frequency = 1; for semi-annual, @Frequency = 2; for quarterly, @Frequency = 4; for bimonthly @Frequency = 6; for monthly, @Frequency = 12. For bonds with @Basis = 'A/364' or 9, you can enter 364 for payments made every 52 weeks, 182 for payments made every 26 weeks, 91 for payments made every 13 weeks, 28 for payments made every 4 weeks, 14 for payments made every 2 weeks, and 7 for weekly payments. @Frequency is an expression of type float or of a type that can be implicitly converted to float.
@Basis
is the type of day count to use. @Basis is an expression of the character string data type category.
|
@Basis
|
Day count basis
|
|
0, 'BOND'
|
US (NASD) 30/360
|
|
1, 'ACTUAL'
|
Actual/Actual
|
|
2, 'A360'
|
Actual/360
|
|
3, 'A365'
|
Actual/365
|
|
4, '30E/360 (ISDA)', '30E/360', 'ISDA', '30E/360 ISDA', 'EBOND'
|
European 30/360
|
|
5, '30/360', '30/360 ISDA', 'GERMAN'
|
30/360 ISDA
|
|
6, 'NL/ACT'
|
No Leap Year/ACT
|
|
7, 'NL/365'
|
No Leap Year /365
|
|
8, 'NL/360'
|
No Leap Year /360
|
|
9, 'A/364'
|
Actual/364
|
|
10, 'BOND NON-EOM'
|
US (NASD) 30/360 non-end-of-month
|
|
11, 'ACTUAL NON-EOM'
|
Actual/Actual non-end-of-month
|
|
12, 'A360 NON-EOM'
|
Actual/360 non-end-of-month
|
|
13, 'A365 NON-EOM'
|
Actual/365 non-end-of-month
|
|
14, '30E/360 NON-EOM', '30E/360 ICMA NON-EOM', 'EBOND NON-EOM'
|
European 30/360 non-end-of-month
|
|
15, '30/360 NON-EOM', '30/360 ISDA NON-EOM', 'GERMAN NON-EOM'
|
30/360 ISDA non-end-of-month
|
|
16, 'NL/ACT NON-EOM'
|
No Leap Year/ACT non-end-of-month
|
|
17, 'NL/365 NON-EOM'
|
No Leap Year/365 non-end-of-month
|
|
18, 'NL/360 NON-EOM'
|
No Leap Year/360 non-end-of-month
|
|
19, 'A/364 NON-EOM'
|
Actual/364 non-end-of-month
|
Return Type
float
Remarks
· If @Settlement is NULL then @Settlement = GETDATE().
· If @Maturity is NULL then @Maturity = GETDATE().
· If @Rate is NULL then @Rate = 0.
· If @Yield is NULL then @Yield = 0.
· If @Redemption is NULL then @Redemption = 100.
· If @Frequency is NULL then @Frequency = 2.
· If @Basis is NULL then @Basis = 0.
· If @Frequency is any number other than 1, 2, 4, 6 or 12, or for @Basis = 'A/364' any number other than 1, 2, 4, 6, or 12 as well as 7, 14, 28, 91, 182, or 364 PRICE returns an error.
· If @Basis is invalid (see above list), PRICE returns an error.
Examples
In this example we calculate the price for a bond maturing on 2034-06-15. The settlement date is 2014-05-01, the yield is 2.76%, the coupon rate is 2.50%, the redemption value is 100, the coupon is paid twice-yearly, and the basis code is 1.
SELECT wct.PRICE(
'2014-05-01', --@Settlement
'2034-06-15', --@Maturity
0.025, --@Rate
0.0276, --@Yield
100, --@Redemption
2, --@Frequency
1 --@Basis
) as PRICE
This produces the following result.
PRICE
----------------------
96.0043799057024
In this example, we calculate the price of a zero-coupon bond.
SELECT wct.PRICE(
'2014-05-01', --@Settlement
'2044-06-15', --@Maturity
0.00, --@Rate
0.0301, --@Yield
100, --@Redemption
2, --@Frequency
1 --@Basis
) as PRICE
This produces the following result.
PRICE
----------------------
40.6583576113141
In this example we calculate the price of a bond settling in the final coupon period.
SELECT wct.PRICE(
'2014-05-01', --@Settlement
'2014-07-15', --@Maturity
0.0190, --@Rate
0.0005, --@Yield
100, --@Redemption
2, --@Frequency
0 --@Basis
) as PRICE
This produces the following result.
PRICE
----------------------
100.380181205142
Here we calculate the price of a bond maturing on the 30th of September 2034, with semi-annual coupons payable on March 30th and September 30th.
SELECT wct.PRICE(
'2014-05-01', --@Settlement
'2034-09-30', --@Maturity
0.0257, --@Rate
0.0269, --@Yield
100, --@Redemption
2, --@Frequency
11 --@Basis
) as PRICE
This produces the following result.
PRICE
----------------------
98.1232907936385
Here's an example of the price calculation with a negative yield.
SELECT wct.PRICE(
'2014-05-01', --@Settlement
'2014-09-30', --@Maturity
0.0257, --@Rate
-0.046219, --@Yield
98, --@Redemption
2, --@Frequency
0 --@Basis
) as PRICE
This produces the following result.
PRICE
----------------------
101.000010706758
This is an example of a bond paying interest every 26 weeks.
SELECT wct.PRICE(
'2014-10-01', --@Settlement
'2023-03-13', --@Maturity
0.1250, --@Rate
0.1100, --@Yield
100, --@Redemption
182, --@Frequency
9 --@Basis
) as PRICE
This produces the following result.
PRICE
----------------------
108.126105929164
See Also