EFV
Updated: 07 February 2011
Use EFV to calculate the future value of a cash flow between two periods. See the Examples for an explanation of how the future value is calculated.
Syntax
SELECT [wctFinancial].[wct].[EFV](
<@StartPer, float,>
,<@Per, float,>
,<@EndPer, float,>
,<@CashflowRate, float,>
,<@EndRate, float,>
,<@Cashflow, float,>)
Arguments
@StartPer
the starting period for the periodic interest rates used in the XFV calculation. Thus, the rate for the period of the cash flow is the rate from the start period to the cash flow period and the rate for the end period is the rate from the start period to the end period. @StartPer is an expression of type float or of a type that can be implicitly converted to float.
@Per
The period in which the cash flows occurs. @Per is an expression of type float or of a type that can be implicitly converted to float.
@EndPer
the ending period for purposes of calculating the future value. The future value is calculated from the cash flow period to the end period. @EndPer is an expression of type float or of a type that can be implicitly converted to float.
@CashflowRate
the periodic interest rate for the cash flow period. Generally, the most obtainable rates are quoted on an annual basis. One way to convert an annual rate to the periodic rate is to divide the annual rate by the number of periods in a year. This should be the interest rate from the start period to the cash flow period. @CashflowRate is an expression of type float or of a type that can be implicitly converted to float.
@EndRate
the annual interest rate for the end period. This should be the interest rate from the start period to the end period. See @CashflowRate for a discussion about converting annual rates to periodic rates. @EndRate is an expression of type float or of a type that can be implicitly converted to float.
@CashFlow
the cash flow value. @CashFlow is an expression of type float or of a type that can be implicitly converted to float.
Return Type
float
Remarks
· The future value will have the same sign as the cash flow amount (@CashFlow).
· If the @CashflowRate is equal to -1, EFV will return a NULL.
· EFV allows positive and negative values for @CashflowRate .
· EFV allows positive and negative values for @EndRate .
· @CashflowRate is the period rate of interest.
· @EndRate is the period rate of interest.
· The @CashflowRate should be the period interest rate from @StartPer to @CashflowPer.
· The @EndRate should be the period interest rate from @StartPer to @EndPer.
· To calculate a future value using dates, try the XFV function.
Examples
In the current period, calculate the future value of a cash flow to be received in one month through to a year from now. The one-month rate is .142%. The one-year rate is .246%
SELECT wct.EFV(
0 --@StartPer
,1 --@Per
,12 --@Per
,.00142/12.00000 --@CashflowRate
,.00246/12.00000 --@EndRate
,100000 --@Cashflow
) as FV
This produces the following result.
FV
----------------------
100234.416482007
(1 row(s) affected)
The result of this calculation means that in the current month, we anticipate that 100,000 received in the next month will be worth approximately 100,234.42 in 12 months, based on the rates provided to the function.
Mathematically, this is the same as the following calculation:
SELECT wct.EFV(
0 --start period
,0 --cash flow period
,12 --end period in one year
,.00000/12.000000 --cash rate
,.00246/12.000000 --one year rate
,1 --cash flow amount
) /
wct.EFV(
0 --start period
,0 --cash flow period
,1 --end period in one month
,.00000/12.000000 --cash rate
,.00142/12.000000 --one month rate
,1 --cash flow amount
) * 100000 as FV
This produces the following result
FV
----------------------
100234.416482004
(1 row(s) affected)
Calculate the future value at the end of five years of a cash flow to be received in six months. The six-month rate is .172% and the 5-year rate is 2.007%
SELECT wct.EFV(
0 --start period
,6 --cash flow period
,60 --end period
,.00172/12.000000 --six-month rate
,.02007/12.000000 --five-year rate
,100000 --cash flow amount
) as FV
This produces the following result.
FV
----------------------
110451.490368559
(1 row(s) affected)
The EFV function can be used in conjunction with the SUM function to calculate the Net Future Value of a collection of cash flows. Let’s say we had the following monthly cash flows and cash flow periods, and we wanted calculate the future value of the cash flows using an annual rate of 2.5%.
SELECT SUM(wct.EFV(
0
,(yr * 12 + mth) -(2011*12 + 1)
,(2012*12 + 2) -(2011*12 + 1)
,0.0250/12.000000
,0.0250/12.000000
,CF)) as SUMFV
FROM (VALUES
(2011,1,-10000),
(2011,2,2000),
(2011,5,1500),
(2011,6,3000),
(2011,10,3800),
(2012,2,2500),
(2012,2,2500)
) n(yr, mth, cf)
This produces the following result.
SUMFV
----------------------
5186.82455474597
(1 row(s) affected)
This is exactly the same result that we would obtain by using the NFV function.
SELECT SUM(wct.EFV(
0
,(yr * 12 + mth) -(2011*12 + 1)
,(2012*12 + 2) -(2011*12 + 1)
,0.0250/12.000000
,0.0250/12.000000
,CF)) as SUMFV
,wct.NFV(0.0250/12.000000
,cf
,yr * 12 + mth) as NFV
FROM (VALUES
(2011,1,-10000),
(2011,2,2000),
(2011,5,1500),
(2011,6,3000),
(2011,10,3800),
(2012,2,2500),
(2012,2,2500)
) n(yr, mth, cf)
This produces the following result.
SUMFV XNFV
---------------------- ----------------------
5189.23863529536 5189.23863529536
(1 row(s) affected)
Unlike the aggregate NFV function, however, by using the SUM and EFV functions, it is possible to calculate the present value of the cash flows using different rates for each cash flow date. In this example, we have a table of rates upon which we do cubic spline interpolation (using the SPLINE_q function from the XLeratorDB/math function library) and join to our cash flows using the appropriate interpolated rate for each date. For illustration purpose, this SQL will show the calculation for each period.
SELECT k.SeriesValue as mdate
,wct.SPLINE_q('SELECT *
FROM (
VALUES
(0, 0),
(1, 0.142),
(3, 0.160),
(6, 0.173),
(12, 0.246),
(24, 0.605),
(36, 1.008)
) r (rdate, annrate)'
,k.SeriesValue) / 1200 as mrate
INTO #r
FROM wct.SeriesInt(0, 36, NULL, NULL, NULL) as k
GO
SELECT *
,wct.EFV(StartPer
,Per
,EndPer
,CashFlowRate
,EndRate
,cf) as FV
FROM(
SELECT 0 as StartPer
,(yr * 12 + mth) -(2011*12 + 1) as Per
,36 as EndPer
,r1.mrate as CashFlowRate
,r2.mrate as EndRate
,cf
FROM (
VALUES
(2011,1,-10000),
(2011,2,2000),
(2011,5,1500),
(2011,6,3000),
(2011,10,3800),
(2012,2,2500),
(2012,2,2500)
) n(yr, mth, cf), #r r1, #r r2
WHERE r1.mdate =(yr * 12 + mth) -(2011*12 + 1)
AND r2.mdate = 36
) m
GO
DROP TABLE #r
GO
This produces the following result.
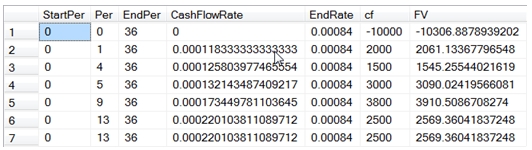
And when we use the SUM function.
SELECT k.SeriesValue as mdate
,wct.SPLINE_q('SELECT *
FROM (
VALUES
(0, 0),
(1, 0.142),
(3, 0.160),
(6, 0.173),
(12, 0.246),
(24, 0.605),
(36, 1.008)
) r (rdate, annrate)'
,k.SeriesValue) / 1200 as mrate
INTO #r
FROM wct.SeriesInt(0, 36, NULL, NULL, NULL) as k
GO
SELECT SUM(
wct.EFV(StartPer
,Per
,EndPer
,CashFlowRate
,EndRate
,cf)) as SUMFV
FROM(
SELECT 0 as StartPer
,(yr * 12 + mth) -(2011*12 + 1) as Per
,36 as EndPer
,r1.mrate as CashFlowRate
,r2.mrate as EndRate
,cf
FROM (
VALUES
(2011,1,-10000),
(2011,2,2000),
(2011,5,1500),
(2011,6,3000),
(2011,10,3800),
(2012,2,2500),
(2012,2,2500)
) n(yr, mth, cf), #r r1, #r r2
WHERE r1.mdate =(yr * 12 + mth) -(2011*12 + 1)
AND r2.mdate = 36
) m
GO
DROP TABLE #r
GO
This produces the following result.
SUMFV
----------------------
5438.75492749465
(1 row(s) affected)
Another interesting way to use the EFV function is in conjunction with the NFV function. The NFV function calculates the future value of all the cash flows passed to the calculation using the maximum period in the set as the anchor. In other words, let’s say that you are looking at a series of cash flows that terminate in 18 months time. The NFV calculation will reflect the NFV as of 18 months from now. If you want to know what the future value will be on at the end of the next year, which is in 23 months time, you can try to add another cashflow to the data for period 23 with an amount of zero, but in many cases it might be easier to use EFV to calculate the future value from period 18 to period 23.
SELECT wct.NFV(.025/12.000000,cfamt,cfdate) as FV
FROM (
VALUES
(5, -100000),
(8, 5000),
(10, 10000),
(12, 15000),
(14, 20000),
(17, 25000),
(18, 30000)
) n(cfdate, cfamt)
This produces the following result.
FV
----------------------
2938.33907229367
(1 row(s) affected)
To calculate the future value to period 23, we could use the following SQL.
SELECT wct.EFV(
0
,18
,23
,.0250/12.000000
,.0250/12.000000
,wct.NFV(.025/12.000000,cfamt,cfdate)) as FV
FROM (
VALUES
(5, -100000),
(8, 5000),
(10, 10000),
(12, 15000),
(14, 20000),
(17, 25000),
(18, 30000)
) n(cfdate, cfamt)
This produces the following result.
FV
----------------------
2969.0745690094
(1 row(s) affected)
Since the rate for EFV and NFV are the same in this example, this is equivalent to the following SQL.
SELECT wct.NFV(.025/12.000000,cfamt,cfdate) as FV
FROM (
VALUES
(5, -100000),
(8, 5000),
(10, 10000),
(12, 15000),
(14, 20000),
(17, 25000),
(18, 30000),
(23, 0)
) n(cfdate, cfamt)
This produces the following result.
FV
----------------------
2969.07456900496
(1 row(s) affected)
Because the periods for the EFV function are declared as float, it is possible to combine the EFV function with YEARFRAC function to calculate the EFV using an annual rate and for different interest bases. For example, if we use the actual/365 interest basis with the YEARFRAC calculation, we will get exactly the same answer as we got in XNFV.
SELECT SUM(wct.EFV(
0
,wct.YEARFRAC('2011-02-07', cf_date, 3)
,wct.YEARFRAC('2011-02-07', '2014-12-31', 3)
,.025
,.025
,cf_amt)) as EFV
,wct.XNFV(.025, cf_amt, cf_date) as XNFV
FROM (
VALUES
('2011-02-07', -80000),
('2011-03-31', -2500),
('2012-03-31', -2500),
('2013-03-31', -2500),
('2014-03-31', -2500),
('2014-12-31', 0)
) n(cf_date, cf_amt)
This produces the following result.
EFV XNFV
---------------------- ----------------------
-98660.6885885387 -98660.6885885387
(1 row(s) affected)
However, if we wanted to use an actual/actual interest basis in the calculation, we simply change the paramter in YEARFRAC and we get a different result than that XNFV calculation.
SELECT SUM(wct.EFV(
0
,wct.YEARFRAC('2011-02-07', cf_date, 1)
,wct.YEARFRAC('2011-02-07', '2014-12-31', 1)
,.025
,.025
,cf_amt)) as EFV
,wct.XNFV(.025, cf_amt, cf_date) as XNFV
FROM (
VALUES
('2011-02-07', -80000),
('2011-03-31', -2500),
('2012-03-31', -2500),
('2013-03-31', -2500),
('2014-03-31', -2500),
('2014-12-31', 0)
) n(cf_date, cf_amt)
This produces the following result.
EFV XNFV
---------------------- ----------------------
-98654.5529721966 -98660.6885885387
(1 row(s) affected)