NELSONSIEGEL
Updated: 31 March 2013
Use the scalar function NELSONSIEGEL to calculate the zero coupon rate for a date from the supplied parameters. Nelson and Siegel suggested calculating the yield curve at a point using this formula:
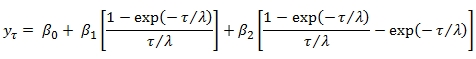
Syntax
SELECT [wctFinancial].[wct].[NELSONSIEGEL](
<@Maturity, float,>
,<@B0, float,>
,<@B1, float,>
,<@B2, float,>
,<@Tau, float,>)
Arguments
@Maturity
The amount of time, in years, to the maturity date. @Maturity is an expression of type float or of a type that can be implicitly converted to float.
@B0
The first factor passed to the function. @B0 is an expression of type float or of a type that can be implicitly converted to float.
@B1
The second factor passed to the function. @B1 is an expression of type float or of a type that can be implicitly converted to float.
@B2
The third factor passed to the function. @B2 is an expression of type float or of a type that can be implicitly converted to float.
@Tau
The fourth factor passed to the function. @Tau is an expression of type float or of a type that can be implicitly converted to float.
Return Type
float
Remarks
· Use the YEARFRAC function to calculate @Maturity.
· Use the NSCOEF function to calculate the @B0, @B1, @B2, and @Tau coefficients to pass into the function.
Examples
In this example, we calculate the interpolated values for maturities 1 through 30. We the SeriesInt function to generate the interpolation points and the NSCOEF function to calculate the coefficients.
SELECT l.SeriesValue as Maturity
,wct.NELSONSIEGEL(
l.seriesvalue --@Maturity
,k.B0 --@B0
,k.B1 --@B1
,k.B2 --@B2
,k.Tau --@Tau
) as Rate
FROM wct.NSCOEF(
'SELECT 1,0.0028 UNION ALL
SELECT 2,0.0056 UNION ALL
SELECT 3,0.0085 UNION ALL
SELECT 5,0.0164 UNION ALL
SELECT 7,0.0235 UNION ALL
SELECT 10,0.0299 UNION ALL
SELECT 20,0.0382 UNION ALL
SELECT 30,0.0406')k
CROSS APPLY wctMath.wct.SERIESINT(1,30,NULL,NULL,NULL) l
This produces the following result.
Maturity Rate
----------- ----------------------
1 0.00298376016908077
2 0.00502183409700056
3 0.00882352652310086
4 0.0129791854798192
5 0.01688451200725
6 0.0203250711182928
7 0.0232655280620921
8 0.0257452146778906
9 0.0278282144583457
10 0.0295809000334999
11 0.0310629320906263
12 0.0323245911890544
13 0.0334068839430623
14 0.0343427004330867
15 0.0351582280427677
16 0.0358742856167667
17 0.0365074605874693
18 0.0370710301382507
19 0.0375756871537565
20 0.038030103897961
21 0.0384413665717732
22 0.0388153095955544
23 0.0391567730501985
24 0.0394698016184686
25 0.0397577990823069
26 0.0400236490213598
27 0.0402698097283141
28 0.0404983893656884
29 0.0407112058966696
30 0.0409098352100148