RANDBINOM
Updated: 31 March 2014
Use the table-valued function RANDBINOM to generate a sequence of random integers from the binomial distribution for a given probability of success @p and a given number of trials @Trials.
Syntax
SELECT * FROM [wctMath].[wct].[RANDBINOM](
<@Rows, int,>
,<@p, float,>
,<@Trials, int,>)
Arguments
@Rows
the number of rows to generate. @MaxIterations must be of the type int or of a type that implicitly converts to int.
@p
the success probability in each trial. @p must be of the type float or of a type that implicitly converts to float.
@Trials
the number of trials. @Trials must be of the type int or of a type that implicitly converts to int.
Return Types
RETURNS TABLE (
[Seq] [int] NULL,
[X] [int] NULL
)
Remarks
· @p must be greater than or equal to zero and less than or equal to 1 (0 <= @p <= 1).
· @Trials must be greater than zero.
· If @p is NULL then @p is set to 0.
· If @Trials is NULL then @Trials is set to 1.
· If @Rows is less than 1 then no rows are returned.
Examples
In this example we create a sequence 1,000,000 random numbers from a binomial distribution with @p = 0.3 and @Trials = 500, COUNT the results, paste then into Excel and graph them.
SELECT
X,
COUNT(*) as [COUNT]
FROM (
SELECT
X
FROM wct.RANDBINOM(
1000000 --@Rows
0.3, --@p
500 --@Trials
)
)n
GROUP BY
X
ORDER BY
1
This produces the following result.
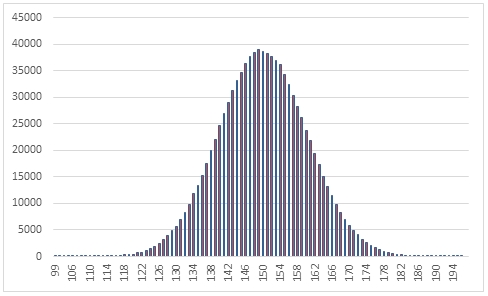
In this example we generate 1,000,000 random numbers from a binomial distribution with probability of .70 and number of trials = 140. We calculate the mean, standard deviation, skewness, and excess kurtosis from the resultant table and compare those values to the expected values for the distribution.
DECLARE @size as int = 1000000
DECLARE @p as float = 0.70
DECLARE @trials as float = 140
DECLARE @mean as float = @p*@trials
DECLARE @var as float = @mean*(1e+00-@p)
DECLARE @stdev as float = SQRT(@var)
DECLARE @skew as float =(1 - 2*@p)/@stdev
DECLARE @kurt as float =(1-6*@p*(1e+00-@p))/@var
SELECT
stat,
[RANDBINOM],
[EXPECTED]
FROM (
SELECT
x.*
FROM (
SELECT
AVG(cast(x as float)) as mean_BINOM,
STDEVP(x) as stdev_BINOM,
wct.SKEWNESS_P(x) as skew_BINOM,
wct.KURTOSIS_P(x) as kurt_BINOM
FROM
wct.RANDBINOM(@size,@p,@trials)
)n
CROSS APPLY(
VALUES
('RANDBINOM','avg', mean_BINOM),
('RANDBINOM','stdev', stdev_BINOM),
('RANDBINOM','skew', skew_BINOM),
('RANDBINOM','kurt', kurt_BINOM),
('EXPECTED','avg',@mean),
('EXPECTED','stdev',@stdev),
('EXPECTED','skew',@skew),
('EXPECTED','kurt',@kurt)
)x(fn_name,stat,val_stat)
)d
PIVOT(sum(val_stat) FOR fn_name in([RANDBINOM],[EXPECTED])) P
This produces the following result (your result will be different).
|
stat
|
RANDBINOM
|
EXPECTED
|
|
avg
|
97.984171
|
98
|
|
kurt
|
-0.009637029
|
-0.008843537
|
|
skew
|
-0.072603649
|
-0.073771111
|
|
stdev
|
5.421933091
|
5.422176685
|
See Also