MSYMMEIG
Updated: 10 May 2016
Use the table-valued function MSYMMEIG to return the D and V matrices representing the eigenvalues and eigenvectors of a real symmetric matrix. The input into the function is a string representation of a real symmetric matrix where the columns are separated by commas and the rows are separated by semicolons. MYSMMEIG returns a single row of two columns containing the string representations of the D and V matrices such that:
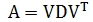
Syntax
SELECT * FROM [wct].[MSYMMEIG](
<@A, nvarchar(max),>)
Arguments
@A
A string representation of the real symmetric matrix.
Return Types
RETURNS TABLE (
[D] [nvarchar](max) NULL,
[V] [nvarchar](max) NULL
)
Remarks
· The string representation of @A must only contain numbers, commas (to separate the columns), and semi-colons to separate the rows.
· Consecutive commas will generate an error.
· Consecutive semi-colons will generate an error.
· Non-numeric data between commas will generate an error.
· Non-numeric data between semi-colons will generate an error.
· To convert a string result to a table, us the table-valued function MATRIX.
Examples
Example #1
In this example we supply @A as a real symmetric matrix and return the D and V matrices.
--Create a real, symmetric matrix
DECLARE @A as varchar(max) = '5,15,55,225;15,55,225,979;55,225,979,4425;225,979,4425,20515'
--Create variables to store the eigenvalues and the eignevectors
DECLARE @D as varchar(max), @V as varchar(max)
--Put the eigenvalues into the D matrix; the eigenvectors into the V matrix
SELECT @D = D, @V = V FROM wct.MSYMMEIG(@A)
--Return the eigenvalues
SELECT @D as D
--Return the eigenvectors
SELECT @V as V
--Only run this SQL to automatically PIVOT the results into the
--traditional row/column matrix presentation
--DECLARE @M as nvarchar(max) = N'SELECT @cols FROM wct.Matrix(@D) d PIVOT(MAX(ItemValue) FOR ColNum in (@cols))p ORDER BY RowNum'
--DECLARE @cols as nvarchar(max)
--SET @cols = (SELECT '[' + cast(ColNum as varchar(max)) + ']' FROM wct.MATRIX(@D) WHERE RowNum = 0 ORDER BY colnum FOR XML PATH(''))
--SET @cols = REPLACE(@cols,'][','],[')
--DECLARE @D_pivot as varchar(max) = REPLACE(REPLACE(@M,'@cols',@cols),'@D','''' + @D + '''')
--EXECUTE(@D_pivot)
--DECLARE @V_pivot as varchar(max) = REPLACE(REPLACE(@M,'@cols',@cols),'@D','''' + @V + '''')
--EXECUTE(@V_pivot)
This produces the following result.
Here are the results formatted as a table.
Example #2
The cross product of any real matrix is a real symmetric matrix. In this example we generate an m-by-n random matrix, calculate the cross product and return the eigenvalues and eigenvectors.
--Create variables to store the eigenvalues and the eignevectors
DECLARE @D as varchar(max), @V as varchar(max)
--Put the eigenvalues into the D matrix; the eigenvectors into the V matrix
SELECT @D = D, @V = V FROM wct.MSYMMEIG(wct.CROSSPROD(wct.MRAND(25,10),NULL))
--Return the eigenvalues
SELECT @D as D
--Return the eigenvectors
SELECT @V as V
--Only run this SQL to automatically PIVOT the results into the
--traditional row/column matrix presentation
--DECLARE @M as nvarchar(max) = N'SELECT @cols FROM wct.Matrix(@D) d PIVOT(MAX(ItemValue) FOR ColNum in (@cols))p ORDER BY RowNum'
--DECLARE @cols as nvarchar(max)
--SET @cols = (SELECT '[' + cast(ColNum as varchar(max)) + ']' FROM wct.MATRIX(@D) WHERE RowNum = 0 ORDER BY colnum FOR XML PATH(''))
--SET @cols = REPLACE(@cols,'][','],[')
--DECLARE @D_pivot as varchar(max) = REPLACE(REPLACE(@M,'@cols',@cols),'@D','''' + @D + '''')
--EXECUTE(@D_pivot)
--DECLARE @V_pivot as varchar(max) = REPLACE(REPLACE(@M,'@cols',@cols),'@D','''' + @V + '''')
--EXECUTE(@V_pivot)
This produces the following result. Your results will be different.
Here are the results formatted as a table.
See Also