QUADDE
Updated: 31 March 2014
Use the scalar function QUADDE to evaluate an infinite integral. QUADDE calculates the integral of the given function f(x) over the interval (-Infinity, Infinity) using Double Exponential Quadrature for non-Periodic functions.
Syntax
SELECT [wctMath].[wct].[QUADDE](
<@Func, nvarchar(max),>
,<@VarName, nvarchar(4000),>
,<@A, sql_variant,>
,<@B, sql_variant,>)
Arguments
@Func
the function to be integrated. @Func is a string containing any valid TSQL statement which includes a single variable that is the object of the integration. The variable name is defined in @VarName. @Func is of a type nvarchar or of any type which implicitly converts to nvarchar.
@VarName
the TSQL variable name. The variable name must start with '@'. @VarName must be of a type nvarchar or a type which implicitly converts to nvarchar.
@A
the lower limit of integration.
@B
the upper limit of integration.
Return Types
float
Remarks
· If @A is not '-Inf' and @B is not 'Inf' then NULL will be returned.
· If @A is '-Inf' then the function will be integrate from –8 to @B.
· If @A is not '-Inf' then the function will be integrated from @A to 8.
· @A can be any floating point number or '-Inf'.
· @B can be any floating point number or 'Inf'.
· If @Func contains an undeclared SQL variable and it is not defined in @VarName a NULL will be returned.
· For best results you should use only non-periodic functions. For periodic functions use QUADOSC instead.
Example
In this example we want to evaluate the integral:
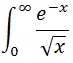
SELECT
devdb.dbo.QUADDE(
'SELECT EXP(-@x)/SQRT(@x)', --@Func
'@x', --@VarName
0, --@A
'Inf' --@B
) as Integral
This produces the following result.
Integral
----------------------
1.77245385090552
In this example we want to evaluate the integral:
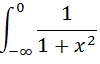
SELECT
devdb.dbo.QUADDE(
'SELECT 1/(1+POWER(@x,2))', --@Func
'@x', --@VarName
'-Inf', --@A
0 --@B
) as Integral
This produces the following result.
Integral
----------------------
1.5707963267949
In this example we want to evaluate the integral:
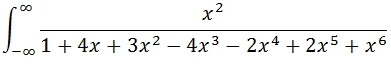
SELECT
devdb.dbo.QUADDE(
'SELECT POWER(@x,2)/(1+4*@x+3*POWER(@x,2)-4*POWER(@x,3)-2*POWER(@x,4)+2*POWER(@x,5)+POWER(@x,6))', --@Func
'@x', --@VarName
'-Inf', --@A
'Inf' --@B
) as Integral
This produces the following result.
Integral
----------------------
3.14159265358979
See Also