VANDERMONDE
Update 03 Mar 2017
Use the scalar function VANDERMONDE to return the Vandermonde matrix. The returned matrix will contain N + 1 columns with the columns representing the geometric progress of the input vector x.
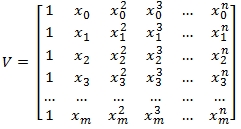
Syntax
SELECT [wct].[VANDERMONDE] (
<@X, nvarchar(max),>
,<@N, int,>)
Arguments
| Input Name | Description |
| @X | The input vector. |
| @N | The upper bound of the Vandermonde matrix. @N is an expression of type int or of a type that can be implicitly converted to int. |
Return Types
[nvarchar](max)
Remarks
Examples
Example #1
VANDERMONDE takes the string representation of the X vector and returns a string value.
SELECT wct.VANDERMONDE('1;2;3;4;5',3)
This produces the following result
Example #2
In this example we use the MATRIX2STRING_q function to create the X vector, the TRANSPOSE function to put that vector into the proper format for the VANDERMONDE function, and the MATRIX function to return the string result as a table in 3rd normal form.
DECLARE @X as nvarchar(max) = wct.MATRIX2STRING_q('SELECT 1,1/2e+0,1/3e+0,1/4e+0,1/5e+0')
SELECT [0],[1],[2],[3],[4],[5]
FROM wct.MATRIX(wct.VANDERMONDE(wct.TRANSPOSE(@X),5))
PIVOT (MAX(ItemValue) FOR ColNum in ([0],[1],[2],[3],[4],[5]))d
ORDER BY RowNum
This produces the following result.
See Also