MINVERSEN_q
Updated: 17 August 2010
Use MINVERSEN_q to calculate the matrix inverse of a square (N x N) array.
For matrices not in normalized form, use the MINVERSE_q function.
Syntax
SELECT * FROM [wctMath].[wct].[MINVERSEN_q] (
<@Matrix_RangeQuery, nvarchar(max),>)
Arguments
@Matrix_RangeQuery
the select statement, as text, used to determine the square (N x N) matrix to be used in this function. The resultant table from the SELECT statement must embody the row number, column number, and data value. The data value returned from the @Matrix_RangeQuery select must be of the type float or of a type that implicitly converts to float.
Return Types
TABLE (
[RowNum] [int] NULL,
[ColNum] [int] NULL,
[ItemValue] [float] NULL
Remarks
· The number of columns in the array must be equal to the number of rows or an error will be returned.
· If the matrix determinant is zero, an error will be returned.
· Use the MINVERSEN function for simpler queries.
· If the array contains NULL, then NULL will be returned.
· The function returns an error if the array contains a non-numeric value.
Examples
In this example, we calculate the matrix product directly from the SELECT statement.
SELECT C.rownum
,C.ColNum
,ROUND(C.ItemValue, 8)
FROM wct.MINVERSEN_q(
'SELECT 0,0,1 UNION ALL
SELECT 0,1,-2 UNION ALL
SELECT 0,2,3 UNION ALL
SELECT 0,3,-4 UNION ALL
SELECT 1,0,5 UNION ALL
SELECT 1,1,5 UNION ALL
SELECT 1,2,7 UNION ALL
SELECT 1,3,8 UNION ALL
SELECT 2,0,9 UNION ALL
SELECT 2,1,10 UNION ALL
SELECT 2,2,11 UNION ALL
SELECT 2,3,12 UNION ALL
SELECT 3,0,13 UNION ALL
SELECT 3,1,14 UNION ALL
SELECT 3,2,15 UNION ALL
SELECT 3,3,16'
) C
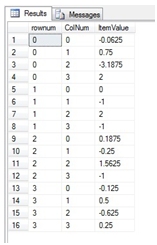
This produces the following result
If we wanted to SELECT data from a TABLE or a VIEW, the SELECT statement would look like this.
CREATE TABLE #i (
MatrixID nvarchar(5),
rowno int,
Colno int,
val float
)
INSERT INTO #i
SELECT '1A',0,0,1.0 UNION ALL
SELECT '1A',0,1,-2.0 UNION ALL
SELECT '1A',0,2,3.0 UNION ALL
SELECT '1A',0,3,-4.0 UNION ALL
SELECT '1A',1,0,5.0 UNION ALL
SELECT '1A',1,1,5.0 UNION ALL
SELECT '1A',1,2,7.0 UNION ALL
SELECT '1A',1,3,8.0 UNION ALL
SELECT '1A',2,0,9.0 UNION ALL
SELECT '1A',2,1,10.0 UNION ALL
SELECT '1A',2,2,11.0 UNION ALL
SELECT '1A',2,3,12.0 UNION ALL
SELECT '1A',3,0,13.0 UNION ALL
SELECT '1A',3,1,14.0 UNION ALL
SELECT '1A',3,2,15.0 UNION ALL
SELECT '1A',3,3,16.0
SELECT C.rownum
,C.ColNum
,ROUND(C.ItemValue, 8)
FROM wct.MINVERSEN_q(
'SELECT rowno
,colno
,val
FROM #i
WHERE MatrixID = ''1A'''
) C
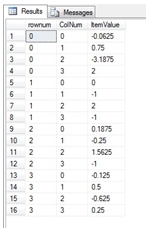
This produces the following result.
If we wanted to return the results in matrix form, we can use the PIVOT function, though this requires knowing the number of columns returned by the function (which is equal to the number of rows).
SELECT [0],[1],[2],[3]
FROM (
SELECT C.rownum
,C.ColNum
,Round(ItemValue, 8) as ItemValue
FROM wct.MINVERSEN_q(
'SELECT 0,0,1 UNION ALL
SELECT 0,1,-2 UNION ALL
SELECT 0,2,3 UNION ALL
SELECT 0,3,-4 UNION ALL
SELECT 1,0,5 UNION ALL
SELECT 1,1,5 UNION ALL
SELECT 1,2,7 UNION ALL
SELECT 1,3,8 UNION ALL
SELECT 2,0,9 UNION ALL
SELECT 2,1,10 UNION ALL
SELECT 2,2,11 UNION ALL
SELECT 2,3,12 UNION ALL
SELECT 3,0,13 UNION ALL
SELECT 3,1,14 UNION ALL
SELECT 3,2,15 UNION ALL
SELECT 3,3,16'
) C
) M PIVOT (
MAX(ItemValue)
FOR colnum IN ([0],[1],[2],[3])
) AS pvt
ORDER BY rownum
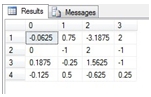
This produces the following result.
In this example, we will use the MINVERSEN_q function and the MMULTN_q function to return the identity matrix.
DECLARE @MString as varchar(4000),
@IString as varchar(4000)
SET @MSTring = 'SELECT 0,0,1 UNION ALL
SELECT 0,1,-2 UNION ALL
SELECT 0,2,3 UNION ALL
SELECT 0,3,-4 UNION ALL
SELECT 1,0,5 UNION ALL
SELECT 1,1,5 UNION ALL
SELECT 1,2,7 UNION ALL
SELECT 1,3,8 UNION ALL
SELECT 2,0,9 UNION ALL
SELECT 2,1,10 UNION ALL
SELECT 2,2,11 UNION ALL
SELECT 2,3,12 UNION ALL
SELECT 3,0,13 UNION ALL
SELECT 3,1,14 UNION ALL
SELECT 3,2,15 UNION ALL
SELECT 3,3,16'
SET @Istring = 'SELECT C.*
FROM wct.MINVERSEN_q(''' + @Mstring + '''
) C'
SELECT [0],[1],[2],[3]
FROM (
SELECT C.rownum
,c.colnum
,round(c.ItemValue, 8) as ItemValue
FROM wct.MMULTN_q(
@Mstring
,@IString
) C
) M PIVOT (
MAX(ItemValue)
FOR colnum IN ([0],[1],[2],[3])
) AS pvt
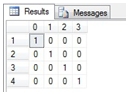
This produces the following result.
See Also