LINEST
Updated: 19 January 2017
Use the table-valued function LINEST to calculate the Ordinary Least Squares (OLS) solution for a series of x- and y-values. The OLS solution calculates a line that best fits the data supplied to the function. The LINEST function returns the statistics that describe the calculated solution, including the coefficients (m), the standard error of the coefficients (se), the t statistic for each coefficient (tstat) and the associated p-values (pval), the coefficient of determination (rsq), the adjusted r-square value (rsqa) and the modified r-square value (rsqm), the standard error of the y estimate (sey), the F-observed value (F), the residual degrees of freedom (df), the regression sum of squares (ss_reg), and the residual some of squares.
In the case where we have one column of x-values and a column of y-values, the OLS solution is immediately recognizable as the formula for a line:
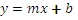
For the purpose of this function, we would re-write the equation as
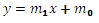
The value for slope, then, is stored in m0.
For purposes of multi-linear regression, where there are multiple columns of x-values (and still a single column of y-values), the formula for the solution is described by the following equation:
Where n is the number of x-columns.
The function expects the input to be in row-column, or spreadsheet, format, rather than in third-normal form. Thus, the input into the function requires the specification of the column names for the x- and y-values, the specification of a 1-based index identifying the column number for the y-values, and a bit value which specifies whether or not the solution has a non-zero y-intercept. The column specifications and the table or view that contains the data are passed into the function as strings. The function dynamically creates SQL and the resultant table from the SQL is used as input into the OLS calculations.
LINEST automatically detects collinearity and removes the right-most co-linear column resulting in a regression coefficient of 0 for that column.
Syntax
SELECT * FROM [wct].[LINEST](
<@TableName, nvarchar(max),>
,<@ColumnNames, nvarchar(4000),>
,<@GroupedColumnName, nvarchar(4000),>
,<@GroupedColumnValue, sql_variant,>
,<@Y_ColumnNumber, int,>
,<@Lconst, bit,>)
Arguments
@TableName
the name, as text, of the table or view that contains the values used in the LINEST calculation.
@ColumnNames
the name, as text, of the columns in the table or view specified by @TableName that contain the values used in the LINEST calculation. Data returned from the @ColumnNames must be of the type float or of a type that implicitly converts to float.
@GroupedColumnName
the name, as text, of the column in the table or view specified by @TableName which will be used for grouping the results.
@GroupedColumnValue
the column value to do the grouping on.
@y_ColumnNumber
the index into the array identifying the column containing the y-values. The index value must be between 1 and n, where n is the number of columns specified in @ColumnNames. @y_ColumnNumber must be of the type int or of a type that implicitly converts to int.
@LConst
A logical value specifying whether to force the y-intercept value (m0) equal to zero. @LConst must be of the type bit or of a type that implicitly converts to bit.
Return Type
RETURNS TABLE (
[stat_name] [nvarchar](10) NULL,
[idx] [int] NULL,
[stat_val] [float] NULL,
[col_name] [nvarchar](128) NULL
)
Table Description
stat_name
Identifies the statistic being returned:
|
m
|
the estimated coefficient
|
|
se
|
the standard error of the estimated coefficient
|
|
tstat
|
the t statistic
|
|
pval
|
the p-value (t distribution) for the t statistic
|
|
rsq
|
the coefficient of determination (r2)
|
|
rsqa
|
adjusted r square
|
|
rsqm
|
multiple r square
|
|
sey
|
the standard error for the y estimate
|
|
f
|
the f-observed value
|
|
df
|
the residual degrees of freedom
|
|
ss_reg
|
the regression sum of squares
|
|
ss_resid
|
the residual sum of squares
|
idx
Identifies the subscript for the estimated coefficient, the standard error of the estimated coefficient, the t statistic, and the p-value. For example, the stat_name m with an idx of 0, specifies that the stat_val is for m0, or the y-intercept (which is b in y = mx + b). An idx of 1 for the same stat_name identifies m1.
The stat_name se with an idx of 0 identifies the standard error of the m0 coefficient (which is sometimes referred to as the standard error of b or seb).
idx values are only supplied for the m, se, tstat, and pval stat_names. All others will have an idx of NULL.
stat_val
the calculated value of the statistic.
col_name
the column name from the resultant table produced by the dynamic SQL. col_name values are produced only for the m, se, tstat, and pval statistics; all other stat_names have NULL for col_name.
Remarks
· If @Lconst is NULL then @Lconst is set to 'True'.
· If @LConst is true than the number of rows must be greater than the number of columns.
· If @Lconst is false than the number of rows must be greater than or equal to the number of columns.
· For more complicated queries, you can try the LINEST_q function.
Examples
Example #1
We put the x- and y-data into a temp table, #xy
SELECT
*
INTO
#xy
FROM (VALUES
(6.1,1.21,4.35,5.42,6.45,138.08)
,(7.95,0.97,2.79,4.73,8.14,80.3)
,(8.53,9.73,9.7,1.16,9.05,284.45)
,(7.4,1.61,9.9,8.8,4.38,226.66)
,(7.42,4.58,0.06,8.97,8.75,112.37)
,(6.19,3.56,9.69,8.7,5.67,168.73)
,(8.44,3.85,8.23,1.05,0.92,160.38)
,(0.84,3.86,7.85,2.14,3.03,129.26)
,(0.37,7.33,5.07,8.06,3.25,170.39)
,(7.48,0.68,8.34,2.98,2.81,188.53)
,(5.33,3.51,7.03,6.49,7.54,131.1)
)n(x1,x2,x3,x4,x5,y)
This is what the data look like.
To invoke the table-valued function LINEST, we enter the following SQL.
SELECT
*
FROM
wct.LINEST(
'#xy', --@TableName
'x1,x2,x3,x4,x5,y', --@ColumnNames
'', --@GroupedColumnName
NULL, --@GroupedColumnValue
6, --@Y_ColumnNumber
'True' --@Lconst
)
Note that the table name and the column names are both bound by single-quotes, so that they are passed into the function as a string. Essentially the function is dynamically creating a SQL statement to SELECT the column names from the #xy table. This means that we can actually simplify the second parameter, since we are selecting all the columns in this particular table, by entering the following:
SELECT
*
FROM
wct.LINEST(
'#xy', --@TableName
*, --@ColumnNames
'', --@GroupedColumnName
NULL, --@GroupedColumnValue
6, --@Y_ColumnNumber
'True' --@Lconst
)
The third parameter is entered as blank (2 single quotes), since there is no column on which we want to group the results for input into the calculation and the fourth parameter is NULL, since there is no grouped column name. The fifth parameter, the y-column value, specifies that the 6th column in the resultant table, which becomes the input into the calculation, contains the y-values. The last parameter specified that we want to calculate the y-interecpt.
The following results are produced.
The results are returned in 3rd normal form. You can use standard SQL commands to re-format the results. For example, if you wanted to produce the the coefficients in a format similar to output of the Excel Data Analyis Regression Tool, you could use the following SQL.
;WITH mycte as (
SELECT *
FROM wct.LINEST('#xy','*','',NULL,6,1)p
)
SELECT
d.col_name
,d.m
,d.se
,d.tstat
,d.pval
,m-wct.T_INV_2T(.05,m.stat_val)*se as [Lower Confidence Level]
,m+wct.T_INV_2T(.05,m.stat_val)*se as [Upper Confidence Level]
FROM mycte p
PIVOT(MAX(stat_val) FOR stat_name in(m,se,tstat,pval))d
CROSS JOIN mycte m
WHERE stat_name = 'df'
AND d.col_name IS NOT NULL
This produces the follwing result.
Similarly, if you wanted to reformat the results to produce the equivalent of the ANOVA table from the Excel Data Analysis Regression tool, you could use the following SQL.
;WITH mycte as (
SELECT
df as [Residual df]
,Obs - df - 1 as [Regression df]
,ss_reg as [Regression SS]
,ss_resid as [Residual SS]
,F
FROM (
SELECT
stat_name
,stat_Val
FROM
wct.LINEST('#xy','*','',NULL,6,1)
WHERE
stat_name in('ss_reg','ss_resid','F','df')
UNION
SELECT
'Obs'
,COUNT(*)
FROM
#xy)d
PIVOT(MAX(stat_val) FOR stat_name in(df,F,ss_reg,ss_resid,Obs))p
)
SELECT
'Regression'
,[Regression df] as DF
,[Regression SS] as SS
,[Regression SS]/[Regression df] as MS
,F
,wct.F_DIST_RT(F,[Regression df],[Residual df]) as [Significance F]
FROM
mycte
UNION ALL
SELECT
'Residual'
,[Residual df]
,[Residual SS]
,[Residual SS]/[Residual df] as [Residual MS]
,NULL
,NULL
FROM
mycte
UNION ALL
SELECT
'Total'
,[Regression df] + [Residual df]
,[Regression SS] + [Residual SS]
,NULL
,NULL
,NULL
FROM
mycte
This produces the following result.
Example #2
Using the same data as Example #1, if we wanted to calculate the coefficients with a y-intercept of 0 we would modify the function call to make the last parameter FALSE. This time, however, we will put the results into a temporary table, #L0, and reformat the results using the #L0 table.
SELECT
*
INTO
#L0
FROM
wct.LINEST(
'#xy', --@TableName
'*', --@ColumnNames
'', --@GroupedColumnName
NULL, --@GroupedColumnValue
6, --@Y_ColumnNumber
'False' --@Lconst
)
The #L0 table should contain the following data.
We can use the same technique as in Example #1 to reformat the coefficient statistics.
SELECT
d.col_name
,d.m
,d.se
,d.tstat
,d.pval
,m-wct.T_INV_2T(.05,m.stat_val)*se as [Lower Confidence Level]
,m+wct.T_INV_2T(.05,m.stat_val)*se as [Upper Confidence Level]
FROM
#L0 p
PIVOT(MAX(stat_val) FOR stat_name in(m,se,tstat,pval))d
CROSS JOIN #L0 m
WHERE
m.stat_name = 'df'
AND d.col_name IS NOT NULL
This produces the following result.
Note that because we specified a 0 intercept an intercept row is still created with a regression coefficient of 0 (keeping the results consistent with the Excel Data Analysis Regression). It is simple enough to exclude this from the output (like R does) simply by adding another conidition to the WHERE clause.
WHERE
m.stat_name = 'df'
AND d.col_name IS NOT NULL
AND d.col_name <> 'Intercept'
The following SQL can be used to reproduce the ANOVA table.
;WITH mycte as (
SELECT
df as [Residual df]
--,Obs - df - 1 as [Regression df]
,Obs - df as [Regression df]
,ss_reg as [Regression SS]
,ss_resid as [Residual SS]
,F
FROM (
SELECT
stat_name
,stat_Val
FROM
#L0
WHERE
stat_name in('ss_reg','ss_resid','F','df')
UNION
SELECT
'Obs'
,COUNT(*)
FROM
#xy)d
PIVOT(MAX(stat_val) FOR stat_name in(df,F,ss_reg,ss_resid,Obs))p
)
SELECT
'Regression'
,[Regression df] as DF
,[Regression SS] as SS
,[Regression SS]/[Regression df] as MS
,F
,wct.F_DIST_RT(F,[Regression df],[Residual df]) as [Significance F]
FROM
mycte
UNION ALL
SELECT
'Residual'
,[Residual df]
,[Residual SS]
,[Residual SS]/[Residual df] as [Residual MS]
,NULL
,NULL
FROM
mycte
UNION ALL
SELECT
'Total'
,[Regression df] + [Residual df]
,[Regression SS] + [Residual SS]
,NULL
,NULL
,NULL
FROM
mycte
This produces the following result.
Note that the calculation of the regression degrees of freedom needs to be adjusted to reflect the 0 intercept. It also worthwhile noting that the calculation in this SQL produces a Significance F that agrees with R while Excel produces a different value (which seems to be caused by subtracting 1 from the residual degrees of freedom).
Example #3
Here’s another example. Instead of just having a matrix of x- and y-values in our table, we are going to add a column, testid, which is a way of grouping x- and y-values together for purposes of doing the LINEST calculation. This allows us to compute the ordinary least square values for multiple sets of data in a single SELECT statement.
Second, we take the x-values and raise them to the powers of 2, 3, 4, 5 thus solving for the equation:
y = B0 + B1x + B2x2 + B3x3 + B4x4 + B5x5
SELECT
*
INTO
#xy
FROM (VALUES
('Wampler5',7590001,0)
,('Wampler5',-20479994,1)
,('Wampler5',20480063,2)
,('Wampler5',-20479636,3)
,('Wampler5',25231365,4)
,('Wampler5',-20476094,5)
,('Wampler5',20489331,6)
,('Wampler5',-20460392,7)
,('Wampler5',18417449,8)
,('Wampler5',-20413570,9)
,('Wampler5',20591111,10)
,('Wampler5',-20302844,11)
,('Wampler5',18651453,12)
,('Wampler5',-20077766,13)
,('Wampler5',21059195,14)
,('Wampler5',-19666384,15)
,('Wampler5',26348481,16)
,('Wampler5',-18971402,17)
,('Wampler5',22480719,18)
,('Wampler5',-17866340,19)
,('Wampler5',10958421,20)
,('Wampler4',75901,0)
,('Wampler4',-204794,1)
,('Wampler4',204863,2)
,('Wampler4',-204436,3)
,('Wampler4',253665,4)
,('Wampler4',-200894,5)
,('Wampler4',214131,6)
,('Wampler4',-185192,7)
,('Wampler4',221249,8)
,('Wampler4',-138370,9)
,('Wampler4',315911,10)
,('Wampler4',-27644,11)
,('Wampler4',455253,12)
,('Wampler4',197434,13)
,('Wampler4',783995,14)
,('Wampler4',608816,15)
,('Wampler4',1370781,16)
,('Wampler4',1303798,17)
,('Wampler4',2205519,18)
,('Wampler4',2408860,19)
,('Wampler4',3444321,20)
,('Wampler3',760,0)
,('Wampler3',-2042,1)
,('Wampler3',2111,2)
,('Wampler3',-1684,3)
,('Wampler3',3888,4)
,('Wampler3',1858,5)
,('Wampler3',11379,6)
,('Wampler3',17560,7)
,('Wampler3',39287,8)
,('Wampler3',64382,9)
,('Wampler3',113159,10)
,('Wampler3',175108,11)
,('Wampler3',273291,12)
,('Wampler3',400186,13)
,('Wampler3',581243,14)
,('Wampler3',811568,15)
,('Wampler3',1121004,16)
,('Wampler3',1506550,17)
,('Wampler3',2002767,18)
,('Wampler3',2611612,19)
,('Wampler3',3369180,20)
,('Wampler2',1,0)
,('Wampler2',1.11111,1)
,('Wampler2',1.24992,2)
,('Wampler2',1.42753,3)
,('Wampler2',1.65984,4)
,('Wampler2',1.96875,5)
,('Wampler2',2.38336,6)
,('Wampler2',2.94117,7)
,('Wampler2',3.68928,8)
,('Wampler2',4.68559,9)
,('Wampler2',6,10)
,('Wampler2',7.71561,11)
,('Wampler2',9.92992,12)
,('Wampler2',12.75603,13)
,('Wampler2',16.32384,14)
,('Wampler2',20.78125,15)
,('Wampler2',26.29536,16)
,('Wampler2',33.05367,17)
,('Wampler2',41.26528,18)
,('Wampler2',51.16209,19)
,('Wampler2',63,20)
,('Wampler1',1,0)
,('Wampler1',6,1)
,('Wampler1',63,2)
,('Wampler1',364,3)
,('Wampler1',1365,4)
,('Wampler1',3906,5)
,('Wampler1',9331,6)
,('Wampler1',19608,7)
,('Wampler1',37449,8)
,('Wampler1',66430,9)
,('Wampler1',111111,10)
,('Wampler1',177156,11)
,('Wampler1',271453,12)
,('Wampler1',402234,13)
,('Wampler1',579195,14)
,('Wampler1',813616,15)
,('Wampler1',1118481,16)
,('Wampler1',1508598,17)
,('Wampler1',2000719,18)
,('Wampler1',2613660,19)
,('Wampler1',3368421,20)
)n(testid,y,x)
Let’s say wanted to run LINEST for the all the data where the testid is equal to Wampler3. We could simply enter the following statement.
SELECT
*
FROM
wct.LINEST(
'#xy' --@TableName
,'y,x,POWER(x,2),POWER(x,3),POWER(x,4),POWER(x,5)' --@ColumnNames
,'testid' --@GroupedColumnName
,'Wampler3' --@GroupedColumnValue
,1 --@Y_ColumnNumber
,'True' --@Lconst
)
This produces the following result.
You will notice that the column names for the calculated columns are Column1, Column2, Column3, and Column4. This is because we have not assigned them a name and these are the default column names. Even though Column1 does not refer to the first column in the resultant table from our dynamic SQL, it is the first column with no name. To get more descriptive column names, you can simply assign the names in the @ColumnNames variable as in this example.
SELECT
*
FROM
wct.LINEST(
'#xy' --@TableName
,'y,x,POWER(x,2) as [x^2],POWER(x,3) as [x^3],POWER(x,4) as [x^4],POWER(x,5) as [x^5]' --@ColumnNames
,'testid' --@GroupedColumnName
,'Wampler3' --@GroupedColumnValue
,1 --@Y_ColumnNumber
,'True' --@Lconst
)
This produces the following result.
In the following SQL we return selected values for each test.
SELECT
p.testid
,p.rsq
,p.rsqa
,p.rsqm
,p.F
,p.df
,p.ss_reg
,p.ss_resid
FROM (
SELECT n.testid,k.stat_name,k.stat_val
FROM (SELECT DISTINCT testid FROM #xy)n
CROSS APPLY wct.LINEST('#xy','y,x,POWER(x,2) as [x^2],POWER(x,3) as [x^3],POWER(x,4) as [x^4],POWER(x,5) as [x^5]','testid',n.testid,1,'True') k
)d
PIVOT(SUM(stat_val) FOR stat_name IN(F,df,ss_reg,ss_resid,rsq,rsqm,rsqa))p
This produces the following result.
In this SQL we select the coefficient statistics for each of the tests.
SELECT
p.testid
,p.col_name
,p.m
,p.se
,p.tstat
,p.pval
FROM (
SELECT
n.testid
,k.stat_name
,k.idx
,k.col_name
,k.stat_val
FROM (
SELECT DISTINCT testid
FROM #xy)n
CROSS APPLY wct.LINEST('#xy','y,x,POWER(x,2) as [x^2],POWER(x,3) as [x^3],POWER(x,4) as [x^4],POWER(x,5) as [x^5]','testid',n.testid,1,'True') k
WHERE k.idx IS NOT NULL
)d
PIVOT(SUM(stat_val) FOR stat_name IN(m,se,tstat,pval))p
ORDER BY
testid
,idx
This produces the following result.
See Also