BlackScholesMertonIV
Updated: 04 Sep 2012
Use BlackScholesMertonIV to calculate an implied volatility for a European-style option using the Black-Scholes-Merton option pricing formula.
Syntax
SELECT [wctOptions].[wct].[BlackScholesMertonIV] (
<@CallPut, nvarchar(4000),>
,<@AssetPrice, float,>
,<@StrikePrice, float,>
,<@TimeToMaturity, float,>
,<@RiskFreeRate, float,>
,<@DividendRate, float,>
,<@Price, float,>)
Arguments
@CallPut
identifies the option as being a call ('C') or a put ('P'). @CallPut is an expression of type nvarchar or of a type that can be implicitly converted to nvarchar.
@AssetPrice
the price of the underlying asset. @AssetPrice is an expression of type float or of a type that can be implicitly converted to float.
@StrikePrice
the exercise price of the option. @StrikePrice is an expression of type float or of a type that can be implicitly converted to float.
@TimeToMaturity
the time to expiration of the option, expressed in years. @TimeToMaturity is an expression of type float or of a type that can be implicitly converted to float.
@RiskFreeRate
the continuously compounded zero-coupon risk-free rate of return over the life of the option. @RiskFreeRate is an expression of type float or of a type that can be implicitly converted to float.
@DividendRate
the continuously compounded zero-coupon dividend rate over the life of the option. For currency options, @DividendRate should be the foreign risk-free interest rate. @DividendRate is an expression of type float or of a type that can be implicitly converted to float.
@Price
the observed price of the option. @Price is an expression of type float or of a type that can be implicitly converted to float.
Return Type
float
Remarks
· @TimeToMaturity must be greater than zero (@TimeToMaturity > 0).
· @AssetPrice must be greater than zero (@AssetPrice > 0).
· @StrikePrice must be greater than zero (@StrikePrice > 0).
· @Price must be greater than zero (@Price > 0).
· If @DividendRate is NULL then @DividendRate = 0.
· If @RiskFreeRate is NULL then @RiskFreeRate = 0.
· To calculate the implied volatility of a European option using the binomial method, use BinomialEuroIV.
Example
Calculate the implied volatility for a call option on 2012-09-04, expiring on 2012-12-15, with a current asset price of 99.5, a strike price of 100 and an observed price of 4.15. The risk free rate is 2% and the dividend rate is 0.5%
SELECT ROUND(wct.BlackScholesMertonIV(
'C' --PutCall
,99.5 --Asset Price
,100 --Strike Price
,datediff(d,'2012-09-04','2012-12-15') / 365.0000 --Time-to-expiry
,.02 --Risk Free Rate
,.005 --Dividend Rate
,4.15 --Price
), 6) as Volatility
This produces the following result.
Volatility
----------------------
0.2
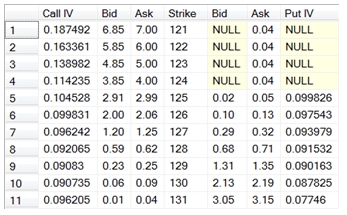
In the following SELECT, we collect the implied volatility for a series of strike prices on EUR/USD option which expire in 7 days time. The opion price is the midpoint of the bid and ask and the 7 day EURIBOR rate is 0.0335700% and the 7 day LIBOR rate is 0.1870000%.
SELECT wct.BlackScholesMertonIV('C'
,127.91 --Asset price
,n.s --Strike
,Cast(7 as float)/cast(365 as float) --Time
,0.000335699 --Continuously Compouned EURIBOR
,0.001869966 --Continuously Compouned LIBOR
,(call_bid + call_ask) / 2 --Price
) as [Call IV]
,cast(n.call_bid as money) as Bid
,cast(n.call_ask as money) as Ask
,n.s as Strike
,cast(n.put_bid as money) as Bid
,cast(n.put_ask as money) as Ask
,wct.BlackScholesMertonIV('P'
,127.91 --Asset price
,n.s --Strike
,Cast(7 as float)/cast(365 as float) --Time
,0.000335699 --Continuously Compouned EURIBOR
,0.001869966 --Continuously Compouned LIBIBOR
,(put_bid + put_ask) / 2 --Price
) as [Put IV]
FROM (
SELECT 6.85, 7.00, 121, NULL, .04 UNION ALL
SELECT 5.85, 6.00, 122, NULL, .04 UNION ALL
SELECT 4.85, 5.00, 123, NULL, .04 UNION ALL
SELECT 3.85, 4.00, 124, NULL, .04 UNION ALL
SELECT 2.91, 2.99, 125, .02, .05 UNION ALL
SELECT 2.00, 2.06, 126, .10, .13 UNION ALL
SELECT 1.20, 1.25, 127, .29, .32 UNION ALL
SELECT 0.59, 0.62, 128, .68, .71 UNION ALL
SELECT 0.23, 0.25, 129, 1.31, 1.35 UNION ALL
SELECT 0.06, 0.09, 130, 2.13, 2.19 UNION ALL
SELECT 0.01, .04, 131, 3.05, 3.15) n(call_bid, call_ask, s, put_bid, put_ask)
This produces the following result.