BinomialPriceNGreeks
Updated: 04 Sep 2012
Use the table-valued function BinomialPriceNGreeks to calculate the price, delta, gamma, theta, vega, rho, and lambda of European or American options using the Binomial Tree option pricing formula.
Syntax
SELECT *
FROM [wctOptions].[wct].[BinomialPriceNGreeks] (
<@CallPut, nvarchar(4000),>
,<@AssetPrice, float,>
,<@StrikePrice, float,>
,<@TimeToMaturity, float,>
,<@RiskFreeRate, float,>
,<@DividendRate, float,>
,<@Volatility, float,>
,<@nSteps, int,>
,<@AmEur, nvarchar(4000),>)
Arguments
@CallPut
identifies the option as being a call ('C') or a put ('P'). @CallPut is an expression of type nvarchar or of a type that can be implicitly converted to nvarchar.
@AssetPrice
the price of the underlying asset. @AssetPrice is an expression of type float or of a type that can be implicitly converted to float.
@StrikePrice
the exercise price of the option. @StrikePrice is an expression of type float or of a type that can be implicitly converted to float.
@TimeToMaturity
the time to expiration of the option, expressed in years. @TimeToMaturity is an expression of type float or of a type that can be implicitly converted to float.
@RiskFreeRate
the annualized, continuously compounded risk-free rate of return over the life of the option. @RiskFreeRate is an expression of type float or of a type that can be implicitly converted to float.
@DividendRate
the annualized, continuously compounded dividend rate over the life of the option. For currency options, @DividendRate should be the foreign risk-free interest rate. @DividendRate is an expression of type float or of a type that can be implicitly converted to float.
@Volatility
the volatility of the relative price change of the underlying asset. @Volatility is an expression of type float or of a type that can be implicitly converted to float.
@nSteps
the number of steps in the binomial tree. @nSteps is an expression of type int or of a type that can be implicitly converted to int.
@AmEur
identifies the option as being American ('A') or European ('E'). @AmEur is an expression of type nvarchar or of a type that can be implicitly converted to nvarchar.
Return Type
float
Remarks
· @TimeToMaturity must be greater than zero (@TimeToMaturity > 0).
· @AssetPrice must be greater than zero (@AssetPrice > 0).
· @StrikePrice must be greater than zero (@StrikePrice > 0).
· @Price must be greater than zero.
· If @DividendRate is NULL an error will be returned
· If @RiskFreeRate is NULL an error will be returned
Example
Calculate the price and Greeks for an American call option on 2012-09-04, expiring on 2012-12-15, with a current asset price of 99.5, a strike price of 100 and a volatility of .20. The risk free rate is 2% and the dividend rate is 0.5%. All column values have been cast as money data types to make the resultant table easier to read.
SELECT Cast(k.Price as money) as Price
,Cast(k.Delta as money) as Delta
,Cast(k.Gamma as money) as Gamma
,Cast(k.Theta as money) as Theta
,Cast(k.Vega as money) as Vega
,Cast(k.Rho as money) as Rho
,Cast(k.Lambda as money) as Lambda
FROM wct.BinomialPriceNGreeks(
'C' --PutCall
,99.5 --Asset Price
,100 --Strike Price
,datediff(d,'2012-09-04','2012-12-15') / 365.0000 --Time-to-expiry
,.02 --Risk Free Rate
,.005 --Dividend Rate
,.20 --Volatility
,100 --Number of steps
,'A' --American/European
) k
This produces the following result.
In the following SELECT, we will populate a derived table with some option information and then calculate the price and greeks for options contained therein. For demonstration purposes we have made lots of simplifying assumptions about the US and contra interest rates and the implied volatility. This just demonstrates the structure of the TSQL statement.
SET NOCOUNT ON
/*Create a temporary table to store data*/
CREATE TABLE #opt (
z char(1),
s money,
ex datetime,
vol money
)
/*Put data in the table*/
INSERT INTO #opt VALUES ('C',98,'2012-09-22',0.23)
INSERT INTO #opt VALUES ('P',99,'2012-09-22',0.15)
INSERT INTO #opt VALUES ('C',100,'2012-09-22',0.15)
INSERT INTO #opt VALUES ('C',101,'2012-09-22',0.21)
INSERT INTO #opt VALUES ('P',102,'2012-09-22',0.19)
INSERT INTO #opt VALUES ('P',98,'2012-10-20',0.18)
INSERT INTO #opt VALUES ('P',99,'2012-10-20',0.24)
INSERT INTO #opt VALUES ('C',100,'2012-10-20',0.21)
INSERT INTO #opt VALUES ('P',101,'2012-10-20',0.25)
INSERT INTO #opt VALUES ('P',102,'2012-10-20',0.25)
INSERT INTO #opt VALUES ('P',98,'2012-11-17',0.17)
INSERT INTO #opt VALUES ('C',99,'2012-11-17',0.24)
INSERT INTO #opt VALUES ('P',100,'2012-11-17',0.17)
INSERT INTO #opt VALUES ('P',101,'2012-11-17',0.25)
INSERT INTO #opt VALUES ('P',102,'2012-11-17',0.22)
INSERT INTO #opt VALUES ('C',98,'2012-12-22',0.21)
INSERT INTO #opt VALUES ('C',99,'2012-12-22',0.19)
INSERT INTO #opt VALUES ('C',100,'2012-12-22',0.21)
INSERT INTO #opt VALUES ('C',101,'2012-12-22',0.15)
INSERT INTO #opt VALUES ('P',102,'2012-12-22',0.22)
INSERT INTO #opt VALUES ('C',98,'2013-03-16',0.24)
INSERT INTO #opt VALUES ('C',99,'2013-03-16',0.17)
INSERT INTO #opt VALUES ('P',100,'2013-03-16',0.2)
INSERT INTO #opt VALUES ('C',101,'2013-03-16',0.19)
INSERT INTO #opt VALUES ('C',102,'2013-03-16',0.21)
INSERT INTO #opt VALUES ('P',98,'2013-03-22',0.16)
INSERT INTO #opt VALUES ('P',99,'2013-03-22',0.25)
INSERT INTO #opt VALUES ('P',100,'2013-03-22',0.23)
INSERT INTO #opt VALUES ('C',101,'2013-03-22',0.22)
INSERT INTO #opt VALUES ('P',102,'2013-03-22',0.16)
/*Select date*/
SELECT O.z
,O.s as Strike
,O.ex as exDate
,O.vol as Volatility
,Cast(k.Price as money) as Price
,Cast(k.Delta as money) as Delta
,Cast(k.Gamma as money) as Gamma
,Cast(k.Theta as money) as Theta
,Cast(k.Vega as money) as Vega
,Cast(k.Rho as money) as Rho
,Cast(k.Lambda as money) as Lambda
FROM #OPT O
CROSS APPLY wct.BinomialPriceNGreeks(
O.z --PutCall
,96.76 --Asset Price
,O.s --Strike Price
,datediff(d,'2012-09-04',O.ex) / 365.0000 --Time-to-expiry
,0.0569 --Risk Free Rate
,0.00284 --Dividend Rate
,O.vol --Volatility
,100 --Number of Steps
,'E' --American/European
) k
/*Clean up table*/
DROP TABLE #opt
For ease of reading, we have reformatted the results.
|
z
|
Strike
|
exDate
|
Volatility
|
Price
|
Delta
|
Gamma
|
Theta
|
Vega
|
Rho
|
Lambda
|
|
C
|
98
|
22-Sep-12
|
0.23
|
1.5321
|
0.4317
|
0.0798
|
-0.0601
|
0.0835
|
0.0198
|
27.2637
|
|
P
|
99
|
22-Sep-12
|
0.15
|
2.521
|
-0.7225
|
0.1042
|
-0.0193
|
0.0713
|
-0.0357
|
-27.7319
|
|
C
|
100
|
22-Sep-12
|
0.15
|
0.3213
|
0.185
|
0.0833
|
-0.0266
|
0.0624
|
0.0087
|
55.7107
|
|
C
|
101
|
22-Sep-12
|
0.21
|
0.4969
|
0.2005
|
0.0622
|
-0.038
|
0.0613
|
0.0093
|
39.0483
|
|
P
|
102
|
22-Sep-12
|
0.19
|
5.2087
|
-0.8785
|
0.0495
|
-0.0095
|
0.0429
|
-0.0445
|
-16.3205
|
|
P
|
98
|
20-Oct-12
|
0.18
|
2.7643
|
-0.5245
|
0.0649
|
-0.019
|
0.139
|
-0.0674
|
-18.3591
|
|
P
|
99
|
20-Oct-12
|
0.24
|
4.1618
|
-0.558
|
0.048
|
-0.0268
|
0.1346
|
-0.0733
|
-12.9729
|
|
C
|
100
|
20-Oct-12
|
0.21
|
1.8125
|
0.3766
|
0.0528
|
-0.035
|
0.127
|
0.0436
|
20.106
|
|
P
|
101
|
20-Oct-12
|
0.25
|
5.5534
|
-0.6412
|
0.0436
|
-0.0249
|
0.1274
|
-0.0852
|
-11.172
|
|
P
|
102
|
20-Oct-12
|
0.25
|
6.2284
|
-0.6827
|
0.0417
|
-0.0227
|
0.1291
|
-0.0911
|
-10.6052
|
|
P
|
98
|
17-Nov-12
|
0.17
|
3.0422
|
-0.4941
|
0.0541
|
-0.0125
|
0.1755
|
-0.1031
|
-15.7167
|
|
C
|
99
|
17-Nov-12
|
0.24
|
3.6311
|
0.4769
|
0.0383
|
-0.0346
|
0.1699
|
0.0862
|
12.7068
|
|
P
|
100
|
17-Nov-12
|
0.17
|
4.1809
|
-0.5985
|
0.0524
|
-0.0102
|
0.163
|
-0.1259
|
-13.8504
|
|
P
|
101
|
17-Nov-12
|
0.25
|
6.1515
|
-0.5902
|
0.0359
|
-0.0193
|
0.1742
|
-0.1282
|
-9.2834
|
|
P
|
102
|
17-Nov-12
|
0.22
|
6.312
|
-0.6451
|
0.0389
|
-0.0139
|
0.1648
|
-0.1393
|
-9.8885
|
|
C
|
98
|
22-Dec-12
|
0.21
|
4.5931
|
0.5339
|
0.0359
|
-0.0272
|
0.2107
|
0.1406
|
11.2477
|
|
C
|
99
|
22-Dec-12
|
0.19
|
3.6944
|
0.4939
|
0.0399
|
-0.025
|
0.2067
|
0.1317
|
12.9365
|
|
C
|
100
|
22-Dec-12
|
0.21
|
3.7
|
0.4639
|
0.0358
|
-0.0263
|
0.2094
|
0.123
|
12.1316
|
|
C
|
101
|
22-Dec-12
|
0.15
|
2.0675
|
0.3869
|
0.0484
|
-0.0192
|
0.2042
|
0.1056
|
18.1071
|
|
P
|
102
|
22-Dec-12
|
0.22
|
6.7402
|
-0.5964
|
0.0334
|
-0.0111
|
0.1988
|
-0.1925
|
-8.5625
|
|
C
|
98
|
16-Mar-13
|
0.24
|
7.4659
|
0.5695
|
0.0233
|
-0.0242
|
0.2759
|
0.2519
|
7.3807
|
|
C
|
99
|
16-Mar-13
|
0.17
|
5.0212
|
0.5415
|
0.0333
|
-0.0193
|
0.2825
|
0.2506
|
10.4356
|
|
P
|
100
|
16-Mar-13
|
0.2
|
5.8236
|
-0.4827
|
0.0284
|
-0.0068
|
0.275
|
-0.2777
|
-8.0206
|
|
C
|
101
|
16-Mar-13
|
0.19
|
4.7036
|
0.4851
|
0.0299
|
-0.02
|
0.2811
|
0.2233
|
9.9784
|
|
C
|
102
|
16-Mar-13
|
0.21
|
4.8521
|
0.4662
|
0.027
|
-0.0212
|
0.2836
|
0.2129
|
9.2962
|
|
P
|
98
|
22-Mar-13
|
0.16
|
3.7663
|
-0.4204
|
0.0343
|
-0.0046
|
0.2799
|
-0.2423
|
-10.8015
|
|
P
|
99
|
22-Mar-13
|
0.25
|
6.7833
|
-0.4488
|
0.0222
|
-0.0103
|
0.2836
|
-0.2737
|
-6.4015
|
|
P
|
100
|
22-Mar-13
|
0.23
|
6.7043
|
-0.4741
|
0.0244
|
-0.0087
|
0.2884
|
-0.2866
|
-6.8428
|
|
C
|
101
|
22-Mar-13
|
0.22
|
5.6755
|
0.4983
|
0.0254
|
-0.022
|
0.282
|
0.232
|
8.4955
|
|
P
|
102
|
22-Mar-13
|
0.16
|
5.8326
|
-0.5547
|
0.0347
|
-0.0025
|
0.2742
|
-0.3243
|
-9.2015
|
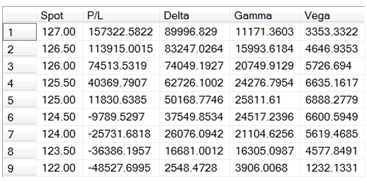
In this example, we translate some of the Greek values into monetary values in order to anticpate how changes in volatility, underlying, and time might affect the profit (or loss) on a long call position with a notional value of 10,000,000, which was bought at 0.50.
DECLARE @notional as float
DECLARE @position as float
SET @position = .50
SET @notional = 10000000
SELECT n.S as Spot
,CAST((k.Price - @position) * @notional/100 as money) as [P/L]
,CAST(k.Delta * @notional/100 as money) as Delta
,CAST(k.Gamma * @notional/100 as money) as Gamma
,CAST(k.Vega * @notional/100 as money) as Vega
FROM (
SELECT 122 UNION ALL
SELECT 123.50 UNION ALL
SELECT 124 UNION ALL
SELECT 124.50 UNION ALL
SELECT 125 UNION ALL
SELECT 125.5 UNION ALL
SELECT 126 UNION ALL
SELECT 126.50 UNION ALL
SELECT 127
) n(s)
CROSS APPLY wct.BinomialPriceNGreeks('C'
,n.s --Asset price
,125 --Strike
,Cast(7 as float)/cast(365 as float) --Time
,0.000335699 --Continuously Compounded EURIBOR
,0.001869966 --Continuously Compounded LIBOR
,.09 --Volatility
,100 --Number of Steps
,'A' --American/European
) k
ORDER BY 1 DESC
This produces the following result