401(k) calculator in SQL Server
Mar
5
Written by:
Charles Flock
3/5/2010 9:09 PM

Using the FV function to calculate the value of your 401(k) when you retire.
In the US, a 401(k) plan refers to a savings plan that allows a worker to contribute part of his salary to a tax-deferred account. Once the worker reaches retirement, withdrawals from the account are taxed as ordinary income. They are called 401(k) plans because they refer to that section of the Internal Revenue Service Code. Employers often incentivize employees to participate by making matching contributions equal to some portion of the employee’s contribution to the plan.
There are many on-line 401(k) calculators and Excel templates for doing 401(k) calculations, but I have never seen one for SQL Server. Bloomberg.com has a good one and we have used that as a starting point. Today, we will demonstrate how to build a 401(k) calculator in T-SQL, and produce a query that returns a result that looks like this:
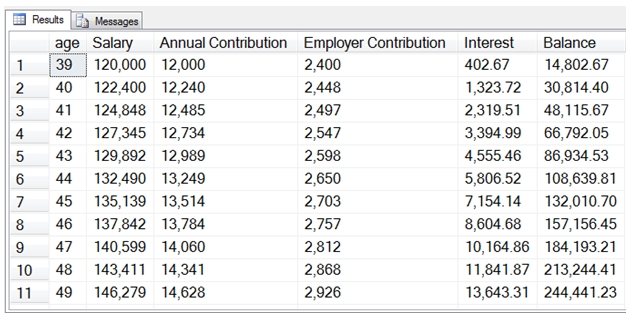
To do this calculation, we want to collect the following data:
· current age,
· retirement age,
· current annual salary,
· anticipated salary growth,
· anticipated employee contribution,
· employer match,
· maximum employer match,
· number of deposit periods in a year,
· anticipated annual earnings, and
· current balance
Current age and retirement age should be self-explanatory. Current annual salary—how much do you earn in a year? Anticipated salary growth—the percentage rate at which you expect your salary to grow each year. Anticipated employee contribution—how much of your annual salary, as a percentage, are you going to put into your 401(k) account? Employer match—how much of your contribution will your employer match. Maximum employer match—the limit on the percentage of salary that the employer will match. Number of deposits per year—how many times per year money is deposited in your 401(k) account. Anticipated annual earnings—the rate of return you expect on your 401(k) balance. Current balance—how much you have in your 401(k) now.
I am going to set this up in a SQL Server 2005 environment. To keep things simple, I will declare variables to keep track of the aforementioned information.
DECLARE @currentage as int, --current age
@retirementage as int, --retirment age
@currentsalary as float, --current salary
@salarygrowth as float, --salary growth as a percentage
@employeecontrib as float, --employee contribution as a percentage of salary
@employermatch as float, --employer match as a percentage of employee contribution
@employermax as float, --maximum employer match as percentage of annual salary
@annualrate as float, --expected annual return
@periods as float, --number of periods per year
@currentbalance as float, --current 401(k) balance
@employerpct as float --see below
Let’s assign some values. Assume that a 39 year-old expecting to retire at 65 earns $120,000/year. Further, since he saved nothing for his retirement, he decides that he needs to be aggressive, so will save 10% of his salary. His employer will match 50% of that up to 4% of his salary. He expects to earn 6% per year on his investments. We would populate the variables as follows:
SET @currentage = 39
SET @retirementage = 65
SET @currentsalary = 120000
SET @salarygrowth = .02
SET @employeecontrib = .10
SET @employermatch = 0.5
SET @employermax = .04
SET @periods = 12
SET @annualrate = .06
SET @currentbalance = 0
We are then going to populate a variable, @employerpct, with the lesser of the employer match multiplied by the employer max and the employee contribution multiplied by the employer match.
SET @employerpct = (
SELECT CASE
WHEN @employeecontrib > @employermax THEN @employermax * @employermatch
ELSE @employeecontrib * @employermatch
END)
I am going to use a common table expression (CTE) to generate the values for each year until retirement age. It’s straightforward to see how to calculate the salary and contribution information for each year.
;WITH mycte as (SELECT
@currentage as age
,@currentsalary as salary
,@currentsalary * @employeecontrib as [Annual Contribution]
,@currentsalary * @employerpct as [Employer Contribution]
UNION ALL
SELECT age + 1
,salary * (1 + @salarygrowth)
,salary * (1 + @salarygrowth) * @employeecontrib
,salary * (1 + @salarygrowth) * @employerpct
FROM mycte
WHERE age < @retirementage - 1)
SELECT *
FROM mycte
This will return a result that looks like this.
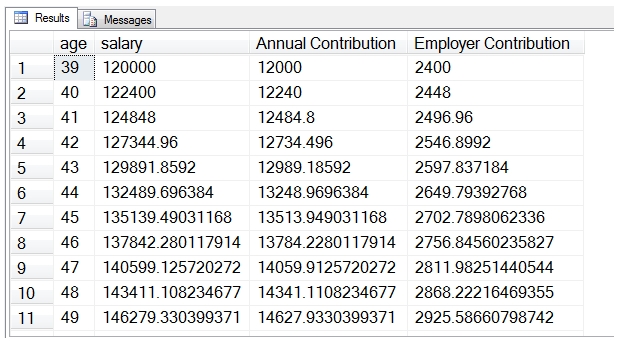
What we really want to calculate, however, is the amount of money that will be available for retirement at the retirement age. To do that, we need to use the FV function.
FV returns the future value of an investment based on periodic, constant payments and a constant interest rate. It is a useful function for doing this kind of analysis. The function requires the following inputs: a rate; the number of periods; the amount of the payment; the present value or lump sum that a series of future payments is worth right now; and a flag that indicates whether the rate is applied at the start of the period or after the end of the period. In other words, is interest earned on the amount in the period in which it is deposited, or starting with the next period?
In this example, the rate is annual rate (.06) and the number of periods is 12. To turn that into a monthly rate we use the following formula:
POWER(1+@annualrate, 1/@periods)-1.
It may seem like we should take the annual rate and divide it by the number of periods. Let’s assume that we have $10,000 at the start of the period and we specified a 6% annual rate. If there are no additions or subtractions to that balance during the course of the year, then the ending value can be calculated as
SELECT wct.FV(.06,1,0,-10000,0)
which returns a value of 10,600, exactly what we would exect with a 6% annual rate. However, if we change this to a monthly rate by simply dividing the annual rate by the number of months
SELECT wct.FV(.06/12,12,0,-10000,0)
we get 10,616.778118645 as a result. This happens because of the effects of monthly compounding, which turned our 6% annual interest into 6.616778% annual interest. In order to compensate for the compounding effect, we enter
SELECT wct.FV(POWER(cast(1.0 as float)+cast(0.06 as float), cast(1.0 as float)/cast(12.0 as float))-1.0,12,0,-10000,0)
which returns 10,600. And, yes, we do have to convert everything to float in order to avoid the implicit conversions in T-SQL.
Finally, the amount of the payment passed into the FV function is the sum of the employee’s annual contribution and the employer’s match divided by the number of periods. The present value is the current balance from the previous row in the CTE.
We must add the FV function to each side of the recursive CTE.
;WITH mycte as (SELECT
@currentage as age
,@currentsalary as salary
,@currentsalary * @employeecontrib as [Annual Contribution]
,@currentsalary * @employerpct as [Employer Contribution]
,wct.FV(POWER(1+@annualrate, 1.0/@periods) - 1,@periods
,-(@currentsalary * @employeecontrib + @currentsalary * @employerpct)/@periods
,-@currentbalance
,0) as Balance
UNION ALL
SELECT age + 1
,salary * (1 + @salarygrowth)
,salary * (1 + @salarygrowth) * @employeecontrib
,salary * (1 + @salarygrowth) * @employerpct
,wct.FV(POWER(1+@annualrate, 1.0/@periods) - 1,@periods
,-(salary * (1 + @salarygrowth) * @employeecontrib + salary * (1 + @salarygrowth) * @employerpct)/@periods
,-Balance
,0)
FROM mycte
WHERE age < @retirementage - 1)
SELECT *
FROM mycte
Below, are the last few lines of the result showing how much will be available for retirement.
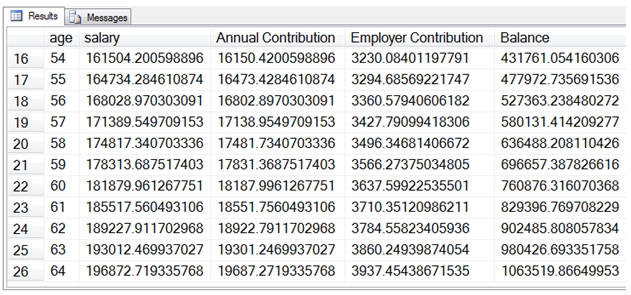
If we wanted to see how much was earned each year, we could change the SELECT statement to the following:
SELECT age
,salary
,[Annual Contribution]
,[Employer Contribution]
,Balance - [Annual Contribution] - [Employer Contribution] - @currentbalance as [Interest]
,Balance
FROM mycte
WHERE age = @currentage
UNION ALL
SELECT B.age
,B.salary
,B.[Annual Contribution]
,B.[Employer Contribution]
,B.Balance - B.[Annual Contribution] - B.[Employer Contribution] - A.Balance
,B.Balance
FROM mycte A, mycte B
WHERE A.age + 1 = B.age
We have now calculated the interest earned in any particular year as the ending balance for that year minus the ending balance for the previous year minus the contributions made during the year and put it in column labeled Interest.
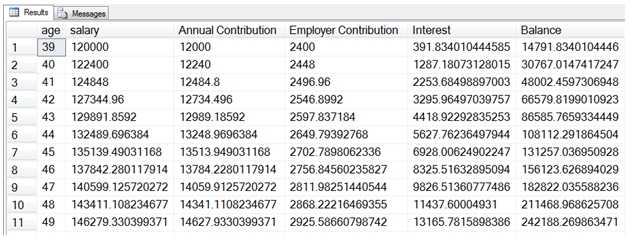
If we wanted the output to be more readable, we can use either the XLeratorDB TEXT function or the FORMATNUM function.
SELECT age
,wct.FORMATNUM(salary, '#,#') as Salary
,wct.FORMATNUM([Annual Contribution], '#,#') as [Annual Contribution]
,wct.FORMATNUM([Employer Contribution], '#,#') as [Employer Contribution]
,wct.FORMATNUM(Balance - [Annual Contribution] - [Employer Contribution] - @currentbalance, '#,#.00') as [Interest]
,wct.FORMATNUM(Balance, '#,#.00') as Balance
FROM mycte
WHERE age = @currentage
UNION ALL
SELECT B.age
,wct.FORMATNUM(B.salary, '#,#')
,wct.FORMATNUM(B.[Annual Contribution], '#,#')
,wct.FORMATNUM(B.[Employer Contribution], '#,#')
,wct.FORMATNUM(B.Balance - B.[Annual Contribution] - B.[Employer Contribution] - A.Balance,'#,#.00')
,wct.FORMATNUM(B.Balance,'#,#.00')
FROM mycte A, mycte B
WHERE A.age + 1 = B.age
Which produces this result
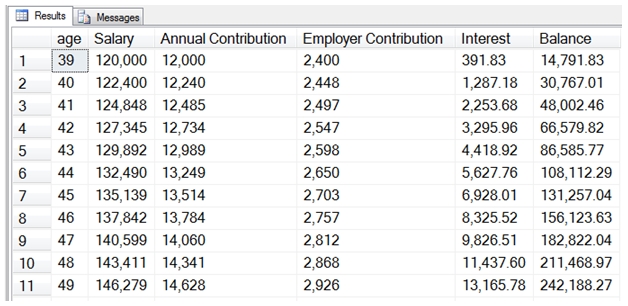
Here are some other statistics that we might want to calculate in relation to the 401(k) contributions:
SELECT 'Employee Contribution', wct.TEXT(sum([Annual Contribution]),'#,###')
from mycte
UNION ALL
SELECT 'Employer Contribution', wct.TEXT(sum([Employer Contribution]), '#,###')
from mycte
UNION ALL
SELECT 'Amount at retirement', wct.TEXT(Balance, '#,###')
FROM mycte
WHERE age = @retirementage - 1
UNION ALL
SELECT 'Ending Salary', wct.TEXT(salary, '#,###')
FROM mycte
WHERE age = @retirementage - 1
UNION ALL
SELECT 'Lifetime earnings', wct.TEXT(a.Balance - sum(b.[Annual Contribution]) - sum(b.[Employer Contribution]), '#,###')
FROM mycte a, mycte b
WHERE a.age = @retirementage - 1
GROUP by a.balance
which produces the following result
It’s great to have this kind of functionality in SQL Server. Whether you want to deliver these calculations to your employees or to potential customers, XLeratorDB makes it simple, efficient and extremely flexible.