What's new in XLeratorDB/Math 1.09
Apr
3
Written by:
Charles Flock
4/3/2014 2:10 PM

The latest release of XLeratroDB/math contains 5 new functions for numerical integration, 12 new functions for the generation of non-uniform random numbers and, for users of SQL Server 2008 and above, 2 new functions for calculating the nth MIN or nth MAX of a data set.
Numerical Integration
Numerical integration, or quadrature, is a technique for approximating the solution of a definite integral
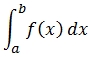
The quadrature functions provided in the math library work in only one dimension.
New Quadrature Functions
· QUAD – Gaussian Adaptive
· QUADGK – Gauss-Kronrod 21-point
· QUADOSC – Double Exponential Oscillatory
QUADGK and QUADTS integrate over a finite interval. QUAD, QUADDE, and QUADOSC integrate over a semi-infinite [a, ], [-, b] or infinite [-,] interval. With the exception of QUADOSC, all the functions have the same signature: a declaration of the function, the name of the variable used in the integration, a lower limit of integration and an upper limit of integration. QUADOSC contains those 4 inputs as well as an oscillatory parameter.
The function definition is an SQL statement defining f(x). It may be a self-contained expression such as SELECT 1/SQRT(@x) and it may reference SQL CLR functions or other user-defined functions such as SELECT 0.92*wct.COSH(@x)-COS(@x), provided that the string is a valid SQL statement which when executed returns a single value.
The variable name is also a string which identifies the variable being evaluated, for example @x. The variable name must be a valid SQL Server variable name. The variable name is always assumed to be a float data type.
For QUADGK and QUADTS the limits of integration are defined as float data types. For the other functions, the limits are defined as sql_variant letting you enter '-Inf'as the lower limit and 'Inf' as the upper limit.
For more information about how the functions work, click on the link to the documentation or read the blog Numerical Integration in SQL Server, Part 1 or Numerical Integration in SQL Server, Part 2.
Non-uniform Random Number Generators
We have never been particularly happy with the RAND() function in SQL Server because it returns only one random number per SELECT statement. Let's say, for example, that you needed to generate 10 uniform random variates. You might think that the following SQL would do just that.
SELECT
x,
RAND() as U
FROM (VALUES (1),(2),(3),(4),(5),(6),(7),(8),(9),(10))n(x)
However what you will get back is 10 rows all with the same value in the column labeled U.
x U
----------- ----------------------
1 0.0131039082850364
2 0.0131039082850364
3 0.0131039082850364
4 0.0131039082850364
5 0.0131039082850364
6 0.0131039082850364
7 0.0131039082850364
8 0.0131039082850364
9 0.0131039082850364
10 0.0131039082850364
Your results will be different, but each row will have the same value as the preceding row. That's why for over 4 years we have had our own RAND function which returns a random number for each row.
SELECT
x,
wct.RAND() as U
FROM (VALUES (1),(2),(3),(4),(5),(6),(7),(8),(9),(10))n(x)
This produces the following result. Again, your results will be different.
x U
----------- ----------------------
1 0.865478075978103
2 0.107120781255477
3 0.1092085615309
4 0.372036924293282
5 0.361355861817187
6 0.907169406724707
7 0.50562595972122
8 0.0924200551083405
9 0.039126692823659
10 0.410970964660389
Previous releases of the math library have included the scalar functions RANDBETWEEN and RANDNORM as well as the table-valued functions SeriesFloat, SeriesDate, and SeriesInt which allow you to generate data sets with millions of random numbers in less than a second.
We have now added 12 new table-valued functions for generating large numbers of non-uniform random numbers simply and quickly. Here's a list of the new functions and the associated distribution.
These non-uniform random number generators use the .NET random number generator, which generates uniform random numbers; we have not implemented a new uniform random number generator.
It has long been possible for XLeratorDB users to generate large numbers of non-uniform random numbers by using XLeratorDB’s table-valued SeriesFloat function and the appropriate inverse distribution function. For example, you could generate a million random gamma deviates using the following SQL.
SELECT
wct.GAMMAINV(SeriesValue,1,1) as x
INTO
#t
FROM
wct.SeriesFloat(0,1,NULL,1000000,'R')
On my laptop this usually takes between 14,800 and 15,000 milliseconds. With the new release of math you can enter the following SQL.
SELECT
x
INTO
#t
FROM
wct.RANDGAMMA(1000000,1,1)
This takes about 2,500 milliseconds on my laptop, an 83% reduction in time, and the SELECT statement is simpler and more intuitive.
All of the new table-valued functions have the same calling structure: the number of rows to return followed by the parameters to the distribution. We use non-uniform random number generators quite extensively in our own system testing and in Monte Carlo simulations. Click on the links to find out more about how these functions work.
MIN/MAX functions
The built-in MAX and MIN functions for SQL Server work quite well for returning the largest or smallest value in a data set. But what if you want the 2nd largest unique value or the 5th smallest unique value? Then things get a bit trickier. While it is certainly possible to obtain those values using T-SQL, the T-SQL statement can be somewhat complicated and can potentially return multiple rows.
These multi-input aggregate functions contain two parameters: the expression to be evaluated and the nth value to be returned.
· MAX – calculated the nth largest unique value in a set.
· MIN – calculates the nth smallest unique value in a set.
Here's a very simple example of where this function might be interesting. Let's say we have a list of baseball players and the number of hits that they recorded in a season. Let's calculate the difference between the largest number of hits and the second largest number of hits. We'll keep the list small for this example, but the same principle would apply if we had a million rows of data instead of eleven rows of data.
SELECT
MAX(n.hits) - wct.MAX(n.hits,2) as MARGIN
FROM (VALUES
('A',181),
('B',210),
('C',200),
('D',206),
('E',215),
('F',210),
('G',183),
('H',188),
('I',207),
('J',185),
('K',184)
)n(player,hits)
This produces the following result.
MARGIN
----------------------
5
And generates the following execution plan.

Of course, you could the calculation in TSQL in any number of ways. Here's one solution in SQL Server 2012.
SELECT TOP 1
MARGIN
FROM (
SELECT
hits,
hits - LAG(hits,1,NULL) OVER (ORDER BY hits ASC) as MARGIN
FROM (VALUES
('A',181),
('B',210),
('C',200),
('D',206),
('E',215),
('F',210),
('G',183),
('H',188),
('I',207),
('J',185),
('K',184)
)n(player,hits)
)p
ORDER BY
hits DESC
This generates the following execution plan.


Here's another solution using a common table expression.
WITH RT(hits,rnk) as(
SELECT
hits,
DENSE_RANK() OVER (ORDER BY HITS DESC) as rnk
FROM (VALUES
('A',181),
('B',210),
('C',200),
('D',206),
('E',215),
('F',210),
('G',183),
('H',188),
('I',207),
('J',185),
('K',184)
)n(player,hits)
)
SELECT DISTINCT
t1.hits-t2.hits as MARGIN
FROM
RT t1
JOIN
RT t2
ON
t1.rnk = 1
AND t2.rnk =2
This generates the following execution plan.
Not only are each of these statements more lines of SQL but, as you can see from the execution plans, the SQL is more complicated which means that your SQL Server is working harder to produce the same result.
Download and try it!
We think that the new functions in the XLeratorDB/math and XLeratorDB/math 2008 libraries add some very interesting capabilities to SQL Server, letting you use T-SQL in novel and interesting ways and letting you do even more sophisticated analysis on your data directly in SQL Server. If you are already an XLeratorDB/math, Suite, or SuitePlus user, just login to your account and download the latest versions for free.
If you are interested in trying out XLeratorDB for yourself download the free 15-day trial now.
If you would like more information, please send us an e-mail at sales@westclintech.com.
See Also