Numerical Integration in SQL Server, Part 1
Mar
31
Written by:
Charles Flock
3/31/2014 4:48 PM

In the latest release of our math library (1.09) we introduce 5 new functions for numerical integration in SQL Server. In this article we explore some of the concepts behind numerical integration and discuss the different techniques used in the new functions, focusing specifically on integration over finite intervals. We will explain some of the general concepts behind numerical integration, also called quadrature, using Simpson's rule, and then look at functions for Gauss-Kronrod, and Tanh-Sinh quadrature. In Part 2, we will look at integration over semi-infinite and infinite intervals.
Numerical integration or quadrature computes an approximate solution to a definite integral
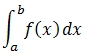
to a given degree of accuracy. For purposes of this article, we are only concerned with one-dimensional integrals.
Let's define a very simple function.
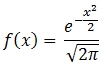
We will create that function in SQL Server using the following SQL.
CREATE FUNCTION [dbo].[f]
(
@x as float
)
RETURNS float
AS
BEGIN
DECLARE @result as float
SET @result = Exp(-@x * @x / 2) / Sqrt(2 * Pi())
RETURN @result
END
GO
We want to evaluate the following integral:
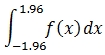
It is possible to come up with an approximation of this integral using a technique called the Composite Simpson rule. It is beyond the scope of this article to go into the math behind Simpson's rule. All we really need to know is that the formula used by Simpson's rule is:
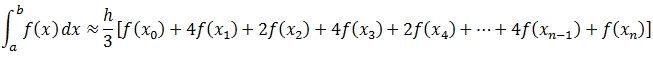
This formula splits the interval [a, b] into n sub-intervals, assigns a weight to each sub-interval (either 1, 2, or 4) and approximates the integral as the sum of the weighted sub-intervals. The length of each subinterval, h, is defined as (b-a)/n.
This technique of breaking up the interval into sub-intervals and summing up the weighted values is common to all quadrature techniques. Simpson's rule is a good place to start as it is reasonably easy to understand and yet robust enough to give quite good results for certain functions.
It is quite straightforward to represent this calculation in SQL Server using the XLeratorDB SeriesFloat function. The following SQL will show the details of the weights and the points at which to evaluate the function f(x) using a value of 10 for n. This illustrates the components of the calculation.
DECLARE @a as float = -1.96
DECLARE @b as float = 1.96
DECLARE @n as float = 10
DECLARE @h as float =(@b - @a) / @n
SELECT seq
,seriesvalue as x
,CASE
WHEN SEQ = 1 THEN 1
WHEN SEQ = @n+1 THEN 1
WHEN SEQ % 2 = 1 THEN 2
ELSE 4
END as w
,dbo.f(SeriesValue) as f
FROM wct.SeriesFloat(@a,@b,@h,@n+1,'L')
This produces the following result.
|
seq
|
x
|
w
|
f
|
|
1
|
-1.96
|
1
|
0.0584409443334515
|
|
2
|
-1.568
|
4
|
0.1166881213013920
|
|
3
|
-1.176
|
2
|
0.1998023735507880
|
|
4
|
-0.784
|
4
|
0.2933858819518050
|
|
5
|
-0.392
|
2
|
0.3694386700816710
|
|
6
|
0
|
4
|
0.3989422804014330
|
|
7
|
0.392
|
2
|
0.3694386700816710
|
|
8
|
0.784
|
4
|
0.2933858819518050
|
|
9
|
1.176
|
2
|
0.1998023735507880
|
|
10
|
1.568
|
4
|
0.1166881213013920
|
|
11
|
1.96
|
1
|
0.0584409443334515
|
With a small change to our SQL, we can approximate the integral directly.
DECLARE @a as float = -1.96
DECLARE @b as float = 1.96
DECLARE @n as float = 10
DECLARE @h as float =(@b - @a) / @n
SELECT
@h*SUM(w*f)/3 as Integral
FROM (
SELECT
CASE
WHEN SEQ = 1 THEN 1
WHEN SEQ = @n+1 THEN 1
WHEN SEQ % 2 = 1 THEN 2
ELSE 4
END as w
,dbo.f(SeriesValue) as f
FROM wct.SeriesFloat(@a,@b,@h,@n+1,'L')
)n
This produces the following result.
Integral
----------------------
0.949973742214864
Let's evaluate that approximation. Using the fundamental theory of calculus part 2, we can calculate the integral as
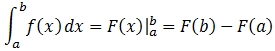
where F(x) is any anti-derivative for f(x).
In our example, the anti-derivative of f(x) is
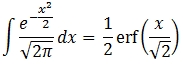
Thus, we can add the exact calculation of the integral to our example and compare the results.
DECLARE @a as float = -1.96
DECLARE @b as float = 1.96
DECLARE @n as float = 10
DECLARE @h as float =(@b - @a) / @n
SELECT
@h*SUM(w*f)/3 as [Approximate Integral]
,0.5*wct.ERF(@b/SQRT(2)) - 0.5*wct.ERF(@a/SQRT(2)) as [Exact Integral]
FROM (
SELECT
CASE
WHEN SEQ = 1 THEN 1
WHEN SEQ = @n+1 THEN 1
WHEN SEQ % 2 = 1 THEN 2
ELSE 4
END as w
,dbo.f(SeriesValue) as f
FROM wct.SeriesFloat(@a,@b,@h,@n+1,'L')
)n
This produces the following result.
Approximate Integral Exact Integral
---------------------- ----------------------
0.949973742214864 0.950004209703556
Generally we can improve upon the approximation by increasing @n. Instead of @n = 10, we set @n = 1,000 and re-run our SQL producing the following result.
Approximate Integral Exact Integral
---------------------- ----------------------
0.950004209703305 0.950004209703556
With n = 1,000 we produce a highly accurate approximation of the definite integral. However, let's see what happens with a slightly different expression that we want to integrate.
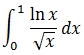
The first thing that should notice is that when x = 0, this function is undefined (which doesn't mean that the integral is undefined). Since we want to integrate from 0 to 1 we need to make some decision about how to evaluate the function at x = 0. Let's see what happens if we integrate from a very small number to 1.
First, we need to change the function in SQL Server.
ALTER FUNCTION [dbo].[f]
(
@x as float
)
RETURNS float
AS
BEGIN
DECLARE @result as float
--SET @result = Exp(-@x * @x / 2) / Sqrt(2 * Pi())
SET @result =LOG(@x)/SQRT(@x)
RETURN @result
END
GO
We also need to know the anti-derivative in order to calculate the integral using the fundamental theory of calculus.
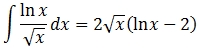
We modify our SQL from the first example and run it.
DECLARE @a as float = POWER(2e+00,-53)
DECLARE @b as float = 1
DECLARE @n as float = 10
DECLARE @h as float =(@b - @a) / @n
SELECT
@h*SUM(w*f)/3 as [Approximate Integral]
,2*SQRT(@b)*(log(@b)-2) - 2*SQRT(@a)*(log(@a)-2) as [Exact Integral]
FROM (
SELECT
CASE
WHEN SEQ = 1 THEN 1
WHEN SEQ = @n+1 THEN 1
WHEN SEQ % 2 = 1 THEN 2
ELSE 4
END as w
,dbo.f(SeriesValue) as f
FROM wct.SeriesFloat(@a,@b,@h,@n+1,'L')
)n
This produces the following result.
Approximate Integral Exact Integral
---------------------- ----------------------
-116218420.298425 -3.99999918368297
As you can see, by making @a very small (2-53 in this case) our Simpson's rule calculation differs significantly from our expected result. And, unlike with our previous example, increasing the value for @n only makes the approximate integral less accurate rather than more accurate.
Alternatively, we can establish a value in the function when x = 0. Here the fundamental theorem of calculus helps us out. The anti-derivative contains the term 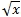 . That will evaluate to zero when x is zero making the value of the anti-derivative at x = 0 zero. Thus, when evaluating the integral in the interval [0,1], we simply need to evaluate F(b). We should just change our SQL Server function to return zero when x = 0.
. That will evaluate to zero when x is zero making the value of the anti-derivative at x = 0 zero. Thus, when evaluating the integral in the interval [0,1], we simply need to evaluate F(b). We should just change our SQL Server function to return zero when x = 0.
ALTER FUNCTION [dbo].[f]
(
@x as float
)
RETURNS float
AS
BEGIN
DECLARE @result as float
--SET @result = Exp(-@x * @x / 2) / Sqrt(2 * Pi())
--SET @result = LOG(@x)/SQRT(@x)
SET @result = CASE @x WHEN 0 THEN 0 ELSE LOG(@x)/SQRT(@x) END
RETURN @result
END
GO
We modify our calculation of the exact integral to only calculate F(b) and we run it.
DECLARE @a as float = 0
DECLARE @b as float = 1
DECLARE @n as float = 10
DECLARE @h as float =(@b - @a) / @n
SELECT
@h*SUM(w*f)/3 as [Approximate Integral]
,2*SQRT(@b)*(log(@b)-2) as [Exact Integral]
FROM (
SELECT
CASE
WHEN SEQ = 1 THEN 1
WHEN SEQ = @n+1 THEN 1
WHEN SEQ % 2 = 1 THEN 2
ELSE 4
END as w
,dbo.f(SeriesValue) as f
FROM wct.SeriesFloat(@a,@b,@h,@n+1,'L')
)n
This produces the following result.
Approximate Integral Exact Integral
---------------------- ----------------------
-1.86339442633272 -4
This answer seems a lot better than the one calculated using a very small number. If we increase @n to 1,000, the approximate integral is returned as -3.60303430482777. If we increase @n to 100,000 the approximate integral is returned as -3.9419728854292. While we are getting closer to the correct answer of -4, this calculation is starting to become computationally expensive. This serves to highlight the fact that while Simpson's rule can be a very good way to demonstrate the principals of numerical integration, it actually has limited real-world utility and there are other, better numerical integration techniques available.
In our latest release of XLeratorDB/math and XLeratorDB/math 2008 we have included 2 new functions for numerical integration over finite intervals: QUADTS and QUADGK. QUADTS is an implementation TANH-SINH quadrature and QUADGK is an implementation of Gaussian-Kronrod 21-point quadrature.
TANH-SINH quadrature is a numerical integration method developed by Hidetosi Takahasi and Masatake Mori. Like Simpson's Rule, TANH-SINH quadrature is the summation of weights and abscissas of the sub-intervals of the interval [a, b]. For Simpson's rule, the weights were either 1, 2, or 4. For TANH-SINH quadrature things are little more complicated. Given the basic quadrature formula:
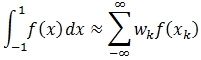
then for TANH-SINH
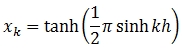
and
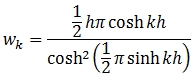
Gauss-Kronrod also uses a summation of the sub-intervals but with a different set of weights and abscissas.
We believe that these two quadratures are the most robust quadrature methods available for definite integrals. We have packaged them up to make the SQL as simple as possible while still providing a high degree of flexibility and performance. Let's see how they work with our preceding examples.
If you go back to the first example, you can see that we created a user-defined function (UDF). While this was not strictly necessary, we did it to make the SQL simpler, especially with respect to integrals over infinite intervals. In QUADTS and QUADGK you enter the function definition as a string, giving you the option of invoking SQL Server built-in functions, user defined functions, and SQL CLR functions, or any combination of them. Additionally if you do not provide alternate definitions for undefined regions of function evaluation (e.g. divide by zero, ln(0), gamma(-1), etc.), these functions will trap the error and set f(x) = 0 at that point.
Let's look at our first example. We would enter the following SQL using QUADTS.
SELECT
wct.QUADTS('SELECT Exp(-@x * @x / 2) / Sqrt(2 * Pi())','@x',-1.96,1.96) as [TANH-SINH]
,0.5*wct.ERF(1.96/SQRT(2)) - 0.5*wct.ERF(-1.96/SQRT(2)) as [Exact Integral]
This produces the following result.
TANH-SINH Exact Integral
---------------------- ----------------------
0.950004209703558 0.950004209703556
The QUADGK function has the same calling structure as the QUADTS. The following SQL returns the results of both quadratures and compares them to the exact integral.
SELECT
wct.QUADTS('SELECT Exp(-@x * @x / 2) / Sqrt(2 * Pi())','@x',-1.96,1.96) as [TANH-SINH]
,wct.QUADGK('SELECT Exp(-@x * @x / 2) / Sqrt(2 * Pi())','@x',-1.96,1.96) as [Gauss-Kronrod]
,0.5*wct.ERF(1.96/SQRT(2)) - 0.5*wct.ERF(-1.96/SQRT(2)) as [Exact Integral]
This produces the following result.
TANH-SINH Gauss-Kronrod Exact Integral
---------------------- ---------------------- ----------------------
0.950004209703558 0.950004209703559 0.950004209703556
Let's see how QUADTS and QUADK handle our second example.
SELECT
wct.QUADTS('SELECT LOG(@x)/SQRT(@x)','@x',0,1) as [TANH-SINH]
,wct.QUADGK('SELECT LOG(@x)/SQRT(@x)','@x',0,1) as [Gauss-Kronrod]
,2*SQRT(1)*(LOG(1)-2) as [Exact Integral]
This produces the following result.
TANH-SINH Gauss-Kronrod Exact Integral
---------------------- ---------------------- ----------------------
-4 -4 -4
As you can see, this is significantly better than what we were able to achieve using Simpson's rule and 100,000 sub-intervals. Additionally, we didn't have to make any special provisions for the function when x = 0.
We also could have used our UDF in the numerical integration.
SELECT
wct.QUADTS('SELECT dbo.f(@x)','@x',0,1) as [TANH-SINH]
,wct.QUADGK('SELECT dbo.f(@x)','@x',0,1) as [Gauss-Kronrod]
,2*SQRT(1)*(LOG(1)-2) as [Exact Integral]
This returns exactly the same result as the previous example.
In all of our examples, we have been able to use the fundamental theorem of calculus to calculate the anti-derivative to verify our calculations. One of the advantages of numerical integration which we haven't explored is that you don't actually need the anti-derivative to perform the integration. For many finite intervals this may be much simpler than calculating the anti-derivative.
Let's look at one more example.
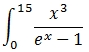
Obviously at x = 0, the function is undefined and for purposes of this example we will set it to zero.
The anti-derivative for this function (which is beyond my ability to calculate by hand) is:
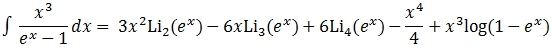
where Lis(z) is the polylogarithm. And the exact solution to the integral is:
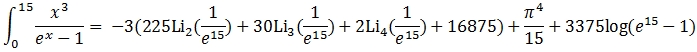
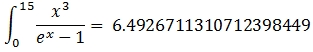
By using the QUADTS or QUADGK function we insulate ourselves from the all that complexity. We can simply enter the following SQL.SELECT
wct.QUADTS('SELECT POWER(@x,3)/(EXP(@x)-1)','@x',0,15) as [TANH-SINH]
,wct.QUADGK('SELECT POWER(@x,3)/(EXP(@x)-1)','@x',0,15) as [Gauss-Kronrod]
This produces the following result, which agrees with the exact solution out to 15 significant digits.
TANH-SINH Gauss-Kronrod
---------------------- ----------------------
6.49267113107124 6.49267113107124
Numerical integration has lots of real-world applications. In fact, one of the reasons that we thought to add these functions to the math library was because of some financial option calculations that we were doing in XLeratorDB/options library. But you can use numerical integration to find the total amount under any curve, to calculate the center of mass, surface area, probabilities, velocity, total work, and many other interesting values. With XLeratorDB you can now take advantage of the fact that you can do these calculations with the data in your SQL Server database using T-SQL, without having to export your data or learn how to use another package or programming language. This lets you integrate extremely powerful analytic capabilities using the tools that you are most comfortable with.
You should download a 15-day free trial today and see how numerical integration could work for you.
See Also