RANDWEIBULL
Updated: 31 March 2014
Use the table-valued function RANDWEIBULL to generate a sequence of random numbers from w Weibull distribution with parameters @Shape and @Scale.
Syntax
SELECT * FROM [wctMath].[wct].[RANDWEIBULL](
<@Rows, int,>
,<@Shape, float,>
,<@Scale, float,>)
Arguments
@Rows
the number of rows to generate. @Rows must be of the type int or of a type that implicitly converts to int.
@Shape
the shape parameter. @Shape must be of the type float or of a type that implicitly converts to float.
@Scale
the scale parameter. @Scale must be of the type float or of a type that implicitly converts to float.
Return Types
RETURNS TABLE (
[Seq] [int] NULL,
[X] [float] NULL
)
Remarks
· @Shape must be greater than zero.
· @Scale must be greater than zero.
· If @Shape is NULL then @Shape is set to 1.
· If @Scale is NULL then @Scale is set to 1.
· If @Rows is less than 1 then no rows are returned.
Examples
In this example we create a sequence of 1,000,000 random numbers rounded to two decimal places from a Weibull distribution with @Shape = 5 and @Scale = 1, COUNT the results, paste them into Excel and graph them.
SELECT
X,
COUNT(*) as [COUNT]
FROM (
SELECT
ROUND(X,2) as X
FROM
wct.RANDWEIBULL(
1000000, --@Rows
5, --@Shape
1 --@Scale
)
)n
GROUP BY
X
ORDER BY
X
This produces the following result.
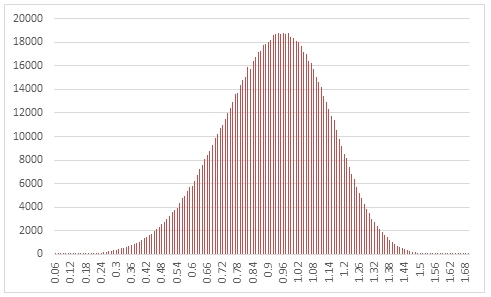
In this example we generate 1,000,000 random numbers from a Weibull distribution with @shape of 0.5 and @scale of 1. We calculate the mean, standard deviation, skewness, and excess kurtosis from the resultant table and compare those values to the expected values for the distribution.
DECLARE @size as int = 1000000
DECLARE @shape as float = 0.5
DECLARE @scale as float = 1
DECLARE @mean as float =
@scale * wct.GAMMA(1e+00 + 1e+00/@shape)
DECLARE @var as float =
POWER(@scale,2)*((wct.GAMMA(1 + 2/@shape) - POWER(wct.GAMMA(1+1/@shape),2)))
DECLARE @stdev as float = SQRT(@var)
DECLARE @skew as float =
(POWER(@scale,3)*wct.GAMMA(1+3/@shape)-3*@mean*@var - POWER(@mean,3))/POWER(@stdev,3)
DECLARE @kurt as float =
(POWER(@scale,4)*wct.GAMMA(1+4/@shape)-4*@skew*POWER(@stdev,3)*@mean-6*POWER(@mean,2)*@var-POWER(@mean,4))/POWER(@stdev,4) - 3
SELECT
stat,
[RANDWEIBULL],
[EXPECTED]
FROM (
SELECT
x.*
FROM (
SELECT
AVG(x) as mean_WEIBULL,
STDEVP(x) as stdev_WEIBULL,
wct.SKEWNESS_P(x) as skew_WEIBULL,
wct.KURTOSIS_P(x) as kurt_WEIBULL
FROM
wct.RANDWEIBULL(@size,@shape,@scale)
)n
CROSS APPLY(
VALUES
('RANDWEIBULL','avg', mean_WEIBULL),
('RANDWEIBULL','stdev', stdev_WEIBULL),
('RANDWEIBULL','skew', skew_WEIBULL),
('RANDWEIBULL','kurt', kurt_WEIBULL),
('EXPECTED','avg',@mean),
('EXPECTED','stdev',@stdev),
('EXPECTED','skew',@skew),
('EXPECTED','kurt',@kurt)
)x(fn_name,stat,val_stat)
)d
PIVOT(sum(val_stat) FOR fn_name in([RANDWEIBULL],[EXPECTED])) P
This produces the following result (your result will be different).
|
stat
|
RANDWEIBULL
|
EXPECTED
|
|
avg
|
1.998743672
|
2
|
|
kurt
|
83.58527068
|
84.72
|
|
skew
|
6.63995163
|
6.618761213
|
|
stdev
|
4.467338077
|
4.472135955
|
See Also