What’s new in XLeratorDB / finance 1.11
Mar
29
Written by:
Charles Flock
3/29/2013 4:53 PM

The latest release of XLeratorDB / finance contains a bunch of new functions for yield curve construction, 2 new bond pricing functions, and an addition to the list of Capital Asset Pricing model formulas.
In the fourth quarter of 2012 on of our clients asked us about constructing a yield curve in SQL Server. We were able to come up with a set-based TSQL solution using the functions in finance 1.10, but after we reviewed it we thought this type of processing was an ideal candidate for a function. We have implemented the SWAPCURVE table-valued function which accepts cash rates, futures prices, and interest rate swap rates as input and returns a table containing the discount factors, zero coupon rates, and continuously compounded zero coupon rates. The function identifies the source of the rates (cash, futures, or swaps) and can also return the interpolated discount factors used to calculate the beginning of the futures strip and in the bootstrapping process.
The SWAPCURVE function uses the cash rates until the beginning of the futures strip and then uses the futures strip until the first swap maturity date to construct the curve. You can read a more detailed explanation about the mechanics of this here.
To make the SWAPCURVE function easier to use, we developed some ‘helper’ functions that convert common abbreviations for dates into actual business dates. The TENOR2DATE function converts common abbreviations like ON, 1W, 1M, and 1Y into dates based upon the spot date and a holiday calendar. Don’t know what the spot date is? You can use the BUSINESSDATE function to calculate the spot date.
The ED_FUT2DATE function converts futures delivery codes into delivery dates. These codes consist of a letter identifying the delivery month and a one- or two-digit number for the year.
The TENOR2DATE function and the ED_FUT2DATE function let you set up your SQL in such a way that you do have to change it every day in order to generate curves on a daily basis.
One of the things that we discovered in building out the SWAPCURVE function it something called the convexity adjustment for futures contracts. We researched it in John C. Hull’s Options Futures & Other Derivatives and reproduced the Ho & Lee convexity adjustment in function called ED_FUT_CONV_ADJ_HL. Two of the inputs to this function are time parameters expressed in fractions of a year giving rise to the ED_FUTYF which turns the futures contract delivery code into a fraction of a year.
You can use all these ‘helper’ function to manipulate the input date into a format consisting of dates (in the case of cash and swaps the maturity dates and in the case of futures the delivery dates), which are then passed directly into the function. They will end up looking something like this
DECLARE @date_start as datetime = '2012-03-15'
SELECT *INTO #curves
FROM (
SELECT '2012-03-16',4.95890410958904E-05,'C' UNION ALL
SELECT '2012-03-19',0.000190143955939201,'C' UNION ALL
SELECT '2012-03-26',0.000350724936480367,'C' UNION ALL
SELECT '2012-06-20',0.0081,'F' UNION ALL
SELECT '2012-07-19',0.00421372954944763,'C' UNION ALL
SELECT '2012-09-19',0.0061,'F' UNION ALL
SELECT '2012-11-19',0.00458179195524779,'C' UNION ALL
SELECT '2012-12-19',0.00484601072792643,'C' UNION ALL
SELECT '2012-12-19',0.02,'F' UNION ALL
SELECT '2013-03-20',0.0165,'F' UNION ALL
SELECT '2013-06-19',0.0062,'F' UNION ALL
SELECT '2013-09-18',0.0141,'F' UNION ALL
SELECT '2013-12-18',0.0109,'F' UNION ALL
SELECT '2014-03-19',0.0177,'F' UNION ALL
SELECT '2014-03-19',0.05656572,'S' UNION ALL
SELECT '2015-03-19',0.060369356592,'S' UNION ALL
SELECT '2016-03-21',0.0687462745090768,'S' UNION ALL
SELECT '2017-03-20',0.0739831312541713,'S' UNION ALL
SELECT '2018-03-19',0.0760236992035542,'S' UNION ALL
SELECT '2019-03-19',0.0854927077565455,'S' UNION ALL
SELECT '2020-03-19',0.0909201712953282,'S' UNION ALL
SELECT '2021-03-19',0.0976838763573592,'S' UNION ALL
SELECT '2022-03-21',0.0991108653966238,'S' UNION ALL
SELECT '2032-03-19',0.101638820387036,'S' UNION ALL
SELECT '2042-03-19',0.1029607869715,'S'
)n(mdate,rate,rsource)
Then we can create the yield curve simply by running the swap curve function and storing the results in a table.
SELECT *
FROM wct.SWAPCURVE(
'SELECT * FROM #curves' --dates, rates, and sources
,@date_start --start date
,2 --Swaps Interest Payment Frequecny
,NULL --Spot Date
,2 --Interest Basis for Cash Rates (A/365)
,2 --Interest Basis for Futures (A/365)
,0 --Interest Basis for Swap Rates (30/360)
,'L' --Interpolation rule for Bootstrapping (Linear)
,'M' --Date Roll Rule (Modified Following)
,NULL --Holidays
)
WHERE rsource <> 'I'
This produces the following result.
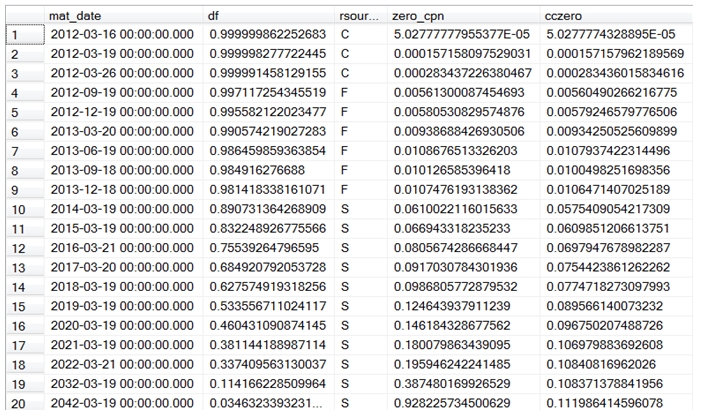
Once the discount factors have been calculated, it is then very straightforward use the discount factors to price and value all future cash flows. The aggregate function DFINTERP consumes the discount factors and returns the interpolated discount factor (using log-linear interpolation) for any date.
If like us, you want to simply create a discount factor for every date for the next 30 or 40 years, you can use the INTERPDFACT table valued function to select the discount factors and specify an interpolation start- and end-date. We found this to be about 25 times faster than calling the DFINTERP function for every day for which we wanted the interpolated rate.
If you just want to calculate a discount factor, zero-coupon, or continuously compounded zero on the fly, from the rates, you can use the ZEROCOUPON function.
Having the ability to easily calculate the zero coupon rates, we also added three functions to support Nelson Siegel interpolation. The NSCOEF table-valued function calculates the Nelson Siegel coefficients which can then be used in the scalar function NELSONSIEGEL to calculate the interpolated zero-coupon for any specified date. THE NSCOEF2 table-valued function provides an alternate, and somewhat slower, way to calculate the coefficients.
We added 2 new functions to our library of bond pricing functions: OFLPRICE and OFLYIELD. These functions are for bonds which have an odd-last and an odd-first coupon payment. You should use these primarily when the bond settles before the first coupon date, as the existing ODDLPRICE and ODDLYIELD functions will handle settlements on or after the first coupon date. There is no harm in using the OFLPRICE and OFLYIELD for settlements after the first coupon, however, as they will simply detect the situation and internally call ODDLPRICE or ODDLPRICE.
Finally, we added the SORTINO2 function to the list of capital asset pricing functions, allowing you to calculate the SORTINO ratio from prices without actually having to calculate the returns before calling the function.
As always, let us know what you think about the new functions and if there is anything you would like to see added to library. If you are an existing use, you can simply log into your account and download the latest version. If you want to try it these new functions first, simply download a 15-day free trial and test them out. If you currently evaluating the product, download a new trial version and let us know what you think.