What’s new in XLeratorDB Math 1.06
Feb
20
Written by:
Charles Flock
2/20/2012 2:59 PM

We have added some performance enhancements to the pseudo-random number generators, as well as a new function to generate random normal numbers.
We created scalar versions of the table-valued matrix functions, making the SQL much simpler and easier to follow. We also added a couple of new matrix functions for forward substitution and back substitution.
In the latest release of XLeratorDB/math and XLeratorDB/math 2008 we have added about two dozen scalar functions for linear algebra, many of which are comparable to the existing table-valued functions found in earlier math releases. The table-valued functions are still there, and in many cases will perform as well or better than the scalar implementations.
We have also tweaked the RAND and RANDBETWEEN functions so that they run a lot faster than in previous versions, and we added a RANDNORM function allowing you to generate pseudo-random numbers using the normal distribution. RANDNORM not only much easier than using the NORMINV and/or NORMSINV function, but is significantly faster. We also enhanced the SeriesFloat function to support random normal as an option in generating a series of random numbers.
Random number improvements
XLeratorDB has always included a RAND() function and a RANDBETWEEN() function, which use the .NET Random Class to return a result. Why do this, when SQL Server already has a built-in RAND() function? The following SQL demonstrates one of the shortcomings of the SQL Server built-in function:
with mycte as
(
select 1 as seq
union all
select seq + 1
from mycte
where seq < 15
)
select seq
,RAND() as [SQL Server RAND function]
FROM mycte
While the actual value for the random number will be different, you will see that the all 15 rows in the resultant table have the same value.
seq SQL Server RAND function
----------- ------------------------
1 0.83355267941491
2 0.83355267941491
3 0.83355267941491
4 0.83355267941491
5 0.83355267941491
6 0.83355267941491
7 0.83355267941491
8 0.83355267941491
9 0.83355267941491
10 0.83355267941491
11 0.83355267941491
12 0.83355267941491
13 0.83355267941491
14 0.83355267941491
15 0.83355267941491
Let’s compare the behavior of the built-in SQL Server function to XLeratorDB function.
with mycte as
(
select 1 as seq
union all
select seq + 1
from mycte
where seq < 15
)
select seq
,RAND() as [SQL Server RAND function]
,wct.RAND() as [XLeratorDB RAND function]
FROM mycte
Again, your random numbers will be different, but you will see that the XLeratorDB function is invoked for every row in the resultant table whereas the built-in SQL Server function in invoked once for the SELECT statement.
seq SQL Server RAND function XLeratorDB RAND function
----------- ------------------------ ------------------------
1 0.444139309225921 0.0687217502959403
2 0.444139309225921 0.876126038507577
3 0.444139309225921 0.0511527941534818
4 0.444139309225921 0.438098561318172
5 0.444139309225921 0.458887217966801
6 0.444139309225921 0.888243296179593
7 0.444139309225921 0.128806069278796
8 0.444139309225921 0.182973967730051
9 0.444139309225921 0.0980124961291151
10 0.444139309225921 0.146008610048462
11 0.444139309225921 0.0532174073695017
12 0.444139309225921 0.476973783652565
13 0.444139309225921 0.558249687159375
14 0.444139309225921 0.525847193682225
15 0.444139309225921 0.0362511808620208
The big improvement in XLeratorDB/math 1.06 is that the RAND function is much faster. Here are the results of some of our tests.
We created a numbers table and put a million rows in it.
CREATE TABLE [dbo].[numbers](
[num] [bigint] NOT NULL,
CONSTRAINT [PK_Numbers] PRIMARY KEY CLUSTERED (
[num] ASC)
)
INSERT INTO Numbers
SELECT seriesvalue
FROM wct.SeriesInt(1, 1000000, NULL, NULL, NULL)
Our perfromance test is then very simple. We selected the million rows we just put into the Numbers table and for each row, we calculate a random number, putting the result into a temp table. We then ran the following SQL to calculate the performance:
SET STATISTICS IO ON
SET STATISTICS TIME ON
select num
,wctMath.wct.RAND() as r
into #r
from Numbers
SET STATISTICS TIME OFF
SET STATISTICS IO OFF
DROP TABLE #r
This produced the following results.
Table 'Numbers'. Scan count 1, logical reads 2112, physical reads 0, read-ahead reads 0, lob logical reads 0, lob physical reads 0, lob read-ahead reads 0.
SQL Server Execution Times:
CPU time = 4400 ms, elapsed time = 4510 ms.
(1000000 row(s) affected)
1,000,000 rows in 4,510 milliseconds is a throughput of 221.7295 rows per millisecond.
When we perform the same test using XLeratorDB/math 1.05, we got the following results:
Table 'Numbers'. Scan count 1, logical reads 2112, physical reads 0, read-ahead reads 0, lob logical reads 0, lob physical reads 0, lob read-ahead reads 0.
SQL Server Execution Times:
CPU time = 166593 ms, elapsed time = 171909 ms.
(1000000 row(s) affected)
In this case, it takes 171,909 milliseconds to process 1,000,000 rows which is a throughput of 5.8170 rows per millisecond.
The XLeratorDB/math 1.06 version of RAND is slightly more than 38 times faster than the previous version. We see the same type of performance improvement in the RANDBETWEEN function.
New random number function
We have added a RANDNORM function in XLeratorDB/math 1.06. The RANDNORM function generates a pseudo-random number along a normal distribution defined by mean and a standard deviation. To use the standard normal distribution, set the mean to zero and that standard deviation to one.
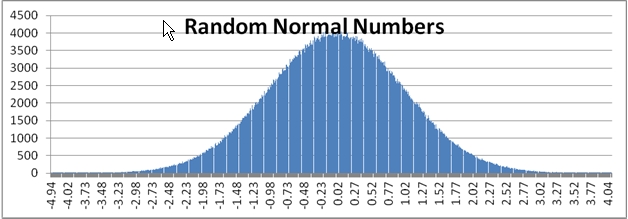
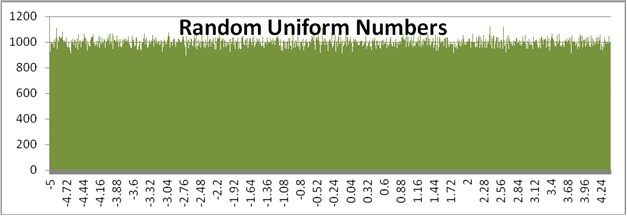
Use the RANDNORM function when you don’t want to generate a uniform distribution of random numbers. Both the RAND function and the RANDBETWEEN function generate random numbers uniformly. What this means, for example, is that in the range -5 to 5, the RANDBETWEEN function is just as likely to generate a -4 as a one or a zero. However, if want to generate a random number along the standard normal distribution, we will generate many more results between -1 and 1 then we will anywhere else in the distribution. We can run the following SQL to and put the results into a graph to contrast the difference.
/*Generate a million Random Normal numbers*/
/*binned by .01 */
SELECT bin
,count(*)
FROM (
SELECT seriesvalue
,ROUND(wct.RANDNORM(0,1), 2) as bin
FROM wct.SeriesInt(1,1000000,NULL,NULL,NULL)
) n
GROUP BY bin
ORDER BY 1 ASC
/*Generate a million Random numbers between -5 and */
/*5 binned by .01 */
SELECT rnd
,COUNT(*)
FROM (
SELECT num
,ROUND(Cast(wct.RANDBETWEEN(-500,500) as float)/CAST(100 as float), 2) rnd
FROM Baseball.dbo.Numbers
) n
GROUP BY rnd
ORDER BY 1 ASC
Here is a comparison graph of the results.
New scalar linear algebra functions
Previous releases of XLeratorDB have included table-valued functions to perform some basic linear algebra computations like matrix multiplication, matrix inversions, the LU decomposition, and the QR decomposition. These functions are still there, and they let you perform quite sophisticated calculations, but the nature of the table-valued functions forces the materialization of interim results, which can make the calculations somewhat unwieldy.
For example, let’s assume that you wanted to do an ordinary least squares calculation using linear algebra. The OLS calculation is defined as:
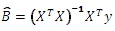
And will return a series of coefficients that satisfies the equation:
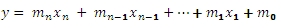
Let’s look first at how we could perform this calculation in XLeratorDB/math 1.06. First, we need a table with some x- and y-values.
|
x1
|
x2
|
x3
|
x4
|
Y
|
|
2310
|
2
|
2
|
20
|
142000
|
|
2333
|
2
|
2
|
12
|
144000
|
|
2356
|
3
|
1.5
|
33
|
151000
|
|
2379
|
3
|
2
|
43
|
150000
|
|
2402
|
2
|
3
|
53
|
139000
|
|
2425
|
4
|
2
|
23
|
169000
|
|
2448
|
2
|
1.5
|
99
|
126000
|
|
2471
|
2
|
2
|
34
|
142900
|
|
2494
|
3
|
3
|
23
|
163000
|
|
2517
|
4
|
4
|
55
|
169000
|
|
2540
|
2
|
3
|
22
|
149000
|
In this table we have 4 columns of x-values and a column of y-values. Since we are going to calculate a y-intercept, we are going to get 5 coefficients returned from our formula.
One way that we could do this, is to put our data into 2 scalar variables, x and y.
DECLARE @x as varchar(max) = '1,2310,2,2,20;
1,2333,2,2,12;
1,2356,3,1.5,33;
1,2379,3,2,43;
1,2402,2,3,53;
1,2425,4,2,23;
1,2448,2,1.5,99;
1,2471,2,2,34;
1,2494,3,3,23;
1,2517,4,4,55;
1,2540,2,3,22'
DECLARE @y as varchar(max) = '142000;
144000;
151000;
150000;
139000;
169000;
126000;
142900;
163000;
169000;
149000'
We can then just do the calculation in a single SELECT statement:
SELECT *
FROM wct.MATRIX(wct.MATMULT(wct.MATINVERSE(wct.MATMULT(wct.TRANSPOSE(@x),@x)),wct.MATMULT(wct.TRANSPOSE(@x),@y)))
This produces the following result.
RowNum ColNum ItemValue
----------- ----------- ----------------------
0 0 52317.8305071266
1 0 27.6413873657511
2 0 12529.7681670853
3 0 2553.21066038766
4 0 -234.237164471067
The MATMULT, MATINVERSE, and TRANSPOSE are scalar functions which take a string representation of a matrix as input into the function and return a string representation of a matrix as output. The string representations use commas and column separators and semi-colons as row separators. The table-valued function MATRIX takes the string representation of the matrix and turns it into a third-normal form table representation. Since the ordinary least squares calculation returns a vector, the ColNum can be excluded from the results. With a slight change to the SQL, we can make the results line up with the OLS equation very nicely.
SELECT 'm' + CAST(RowNum as varchar(2)) as coefficient
,ItemValue as Val
FROM wct.MATRIX(wct.MATMULT(wct.MATINVERSE(wct.MATMULT(wct.TRANSPOSE(@x),@x)),wct.MATMULT(wct.TRANSPOSE(@x),@y)))
This produces the following result.
coefficient Val
----------- ----------------------
m0 52317.8305071266
m1 27.6413873657511
m2 12529.7681670853
m3 2553.21066038766
m4 -234.237164471067
Let’s contrast this by using the existing table-valued functions to perform the same calculation.
SELECT *
INTO #xy
FROM (VALUES
(0,2310,2,2,20,142000),
(1,2333,2,2,12,144000),
(2,2356,3,1.5,33,151000),
(3,2379,3,2,43,150000),
(4,2402,2,3,53,139000),
(5,2425,4,2,23,169000),
(6,2448,2,1.5,99,126000),
(7,2471,2,2,34,142900),
(8,2494,3,3,23,163000),
(9,2517,4,4,55,169000),
(10,2540,2,3,22,149000)
) n(r, x1, x2, x3, x4, y)
In this table we have 4 columns of x-values and a column of y-values. The r column is simply a way to uniquely identify the row. Since we are going to calculate a y-intercept, we are going to get 5 coefficients returned from our formula.
We will populate a table, #xprime, with the x-values, including an extra column of all ones, to account for the y-intercept.
SELECT r, c, xx
INTO #xprime
FROM (SELECT r,1 as x0,x1, x2, x3, x4 FROM #xy) n1
CROSS APPLY(VALUES
('0', x0),
('1', x1),
('2', x2),
('3', x3),
('4', x4)
) x(c, xx)
We then mulitply the transposed #xprime by #xprime and store that in #x_xprime.
SELECT *
into #x_xprime
FROM wct.MMULTN_q(
'SELECT c,r,xx FROM #xprime'
,'SELECT r,c,xx from #xprime'
)
We take the inverse of that and store it in #x_xprime_inverse.
SELECT *
into #x_xprime_inverse
FROM wct.MINVERSEN_q('SELECT RowNum, ColNum, ItemValue from #x_xprime')
We multiply the transposed #x_prime values by the y-values and store that in #xprime_y.
SELECT *
into #xprime_y
FROM wct.MMULTN_q(
'SELECT c,r,xx FROM #xprime'
,'SELECT r,0,y from #xy'
)
And now we can calculate the regression coefficients.
SELECT 'm' + Cast(RowNum as varchar) as coefficient
,ItemValue
FROM wct.MMULTN_q(
'SELECT RowNum,ColNum,ItemValue from #x_xprime_inverse'
,'SELECT RowNum,ColNum,ItemValue from #xprime_y'
)
This produces the following result.
coefficient ItemValue
------------------------------- ----------------------
m0 52317.8305073259
m1 27.6413873659951
m2 12529.7681670867
m3 2553.21066039095
m4 -234.237164471189
As you can see, there is no difference in the results. However, until now, it was not possible to do the calculation in a single select statement, and we had to create a number of temporary tables, which we then have to clean up when we are done.
In many situations you will need much less SQL with the scalar functions versus the table-valued functions. For larger matrices, however, the table-valued functions will perform better than the scalar functions, because converting to and from the string representation of the matrices is a relatively expensive operation. You can decide which works best in your environment.
We also created a number of functions to convert table-valued output into the string representation of the matrix: you can use MATRIX2STRING to convert a de-normalized table to a string and NMATRIX2STRING to convert a third-normal form table to a string. We also have created functions to materialize (as a string) the identity matrix (EYE), a matrix of ones (ONES), and matrix of zeroes (ZERO), a matrix of random numbers (MRAND), and a matrix of random normal numbers (MRANDN) .
There are functions that extract data from the string representation of the matrix. DIAG takes the diagonal of the matrix; MTRIL creates the lower triangular matrix of the input matrix; MTRIU takes the upper triangular matrix of the input matrix.
Finally, we created scalar versions of the QR decomposition (QR) and the LU decomposition (LU) as well as creating a matrix addition function (MATADD) and a matrix subtraction function (MATSUB) a forward substitution function (FWDSUB) and a backward substitution function (BKSUB).
If you are already using the math library, you can download the latest version for free. If you are not already using XLeratorDB, try the 15-day free trial today and discover how you can analyze big data in your SQL Server database.