Loan Calculations in EXCEL
May
10
Written by:
Charles Flock
5/10/2010 5:59 PM

EXCEL 2010 [beta] documentation uses the phrase ‘the following functions have improved accuracy.’ But what does that actually mean in relation to the IPMT, PPMT, CUMPRINC, and CUMIPMT functions?
The official blog of the Microsoft Excel product team has an item entitled Function Improvements in EXCEL 2010. The blog states that the following financial functions have improved accuracy: CUMIPMT; CUMPRINC; IPMT; PMT and PPMT. Since XLeratorDB delivers comparable functionality to SQL Server, we were curious as to what that “improved accuracy” actually delivered in the beta version of EXCEL 2010.
We have tested our functions against EXCEL functions millions of times … literally. Usually we have about a million test cases for each function and we calculate the results in EXCEL and compare them to our results in SQL Server. Sometimes we discover that EXCEL functions are unreliable in certain conditions, but for the most part XLeratorDB functions and EXCEL functions produce the same results. Where they do not, we document the differences and may even write a blog or post a video about it.
Sometimes, we are relatively unhappy with the way an EXCEL functions works, and we have to decide whether we want to mimic the EXCEL functionality or go our own way. This is always a big decision for us; there is something like 500 million EXCEL users and you would think that any problems in the EXCEL calculations would be well documented and fixed long ago. Functions like IPMT and PPMT have been around a long time.
Let’s look at some of the things that we uncovered in the basic functions related to interest payments on a loan. Here’s an EXCEL 2007 worksheet where we entered some test data and calculated IPMT, PPMT and PMT.
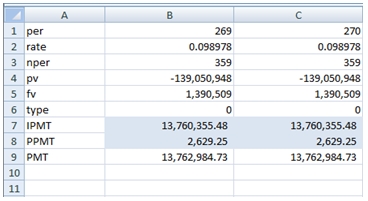
Column B shows the Excel calculations for the 269th payment on a loan, while Column C is for the 270th payment. As you can see, the IPMT and PPMT amounts are the same for each of the payments. That seems very odd, given that the 269th payment clearly includes a principal reduction of $2629.25. Therefore, the interest on the 270th payment should be less, since the principal amount is less. In addition the principal payment should be more in period 270, since the payment amount stays the same and the interest amount should be less.
Before diving too deeply into the math behind this, let’s just use EXCEL 2010 to perform the same calculations.
EXCEL 2007 EXCEL 2010 beta
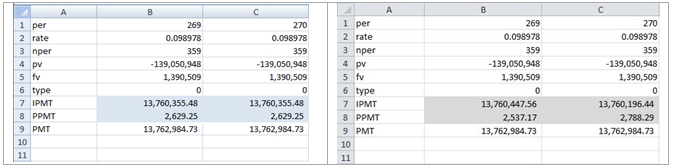
Clearly, the EXCEL 2010 calculations are different. That presents an interesting challenge; Which version is correct?
Let’s look at the math. The calculation of the interest payment amount in any period is straightforward: it’s principal * rate. The challenge, then, is knowing the principal amount.
The principal amount is the present value of the future cash flows for the loan. We can use another EXCEL function, the PV calculation, to determine the principal amount at the beginning of each period. We just need to calculate remaining life of the loan, which is the difference between the number of periods in the loan and the period for which we want to calculate the interest payment. We can enter the following formula in B10:
=-PV(B2,B3-B1+1,B9,B5,B6)
In B11, we will calculate the interest payment amount by entering the following formula:
=B2*B10
We can then copy B10:B11 to C10:C11. I have entered these “manually constructed” formulae in both versions of EXCEL and here are the results of those calculations:
EXCEL 2007 EXCEL 2010 beta
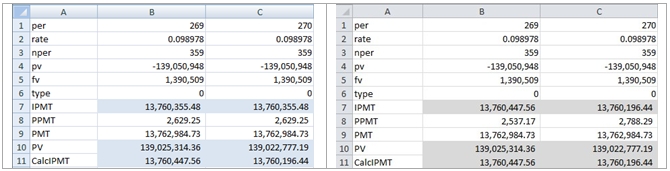
As you can see, the results of the IPMT calculation in the EXCEL 2010 beta agrees with the formulae that we entered in row 11. You can also see that the calculations in row 11 in EXCEL 2007 and EXCEL 2010 beta agree, but that the results of the IPMT calculation in EXCEL 2007 do not agree. We can conclude that the IPMT calculation in EXCEL 2007 is inaccurate.
Let’s look at the PPMT calculation. The principal payment on a loan is the difference between the payment amount (which we have calculated in row 8) and the interest payment amount (which we have just recalculated). Since we have just determined that the EXCEL 2007 IPMT calculation is inaccurate, it seems unlikely that the PPMT calculation in EXCEL 2007 will be accurate, but we also want to verify the EXCEL 2010 beta calculation. In cell B12 we enter:
=B9-B11
and copy it to C11. We do the same thing in the EXCEL 2010 beta. Here are the results:
EXCEL 2007 EXCEL 2010 beta
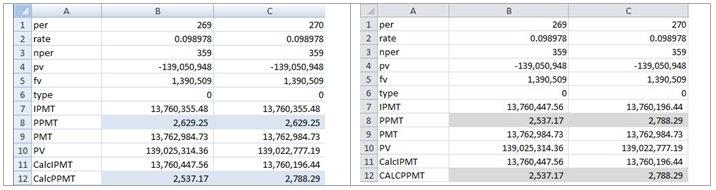
Again, we see that the formulae we constructed manually agrees in both worksheets and that they agree with the EXCEL 2010 beta PPMT calculation. We have to conclude that the EXCEL 2007 PPMT calculation is inaccurate.
This is good news for users of EXCEL 2010. It is finally gaining the reliability for financial calculations that EXCEL users have always depended on (and assumed they had). I guess the users of previous versions of EXCEL are screwed, though. These calculations may well be embedded in important legal documents or provide the foundation for critical budget projections. It leaves us wondering and worrying: Should we go back and verify every important interest calculation or should we just pony up the money for EXCEL 2010, and spend a lot more money trying to reconcile the differences? It’s a tough call.
Is there any way to know where to look for potential problems with the IPMT and PPMT calculations? We noticed that the problem only occurs in loans that have a non-zero future value and that it occurs in the latter part of the loan. It’s hard for us to narrow it down any further. I would have thought that the phrase ‘improved accuracy’ meant that we were talking about the accuracy to a greater number of significant digits. This seems more like saying that EXCEL accurately produces the correct answer more frequently. Not exactly a comforting thought.
Now that we have determined that EXCEL’s IPMT and PPMT functions may be unreliable, let’s look at the CUMPRINC and CUMIPMT functions, which calculate the cumulative principal payments and cumulative interest payments. Given the problems with PPMT and IPMT in EXCEL 2007, we shouldn’t be surprised if the results are inaccurate in EXCEL 2007, but let’s check the EXCEL 2010 beta. In cell B13 we enter:
=CUMPRINC(B2,B3,-B4-B5,1,B1,B6)
and in cell B14 we enter:
=CUMIPMT(B2,B3,-B4,1,B1,B6)
We then copy B13:B14 to C13:C14.
EXCEL 2007 EXCEL 2010 beta
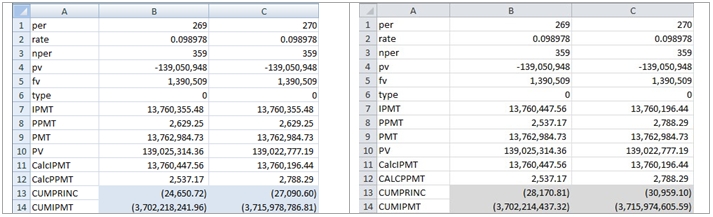
Unsurprisingly, EXCEL 2007 and EXCEL 2010 beta do not agree. How do we verify the accuracy of the functions?
It seems like the simplest way to verify the CUMPRINC function is to simply add up all the PPMT calculations from inception to the specified period. The array formula capability of EXCEL makes this quite easy. In cell B15, enter
=SUM(PPMT(B2,ROW(D1:D269),B3,B4,B5,B6))
and then press CTRL+SHIFT+ENTER. If you hit enter, when you entered the formula, just edit the formula (F2) and press CTRL+SHIFT+ENTER. This stores the sum of the PPMT calculation for the first 269 payments. In cell C15 we enter:
=SUM(PPMT(C2,ROW(D1:E270),C3,C4,C5,C6))
and then press CTRL+SHIFT+ENTER. Here are the results:
EXCEL 2007 EXCEL 2010 beta
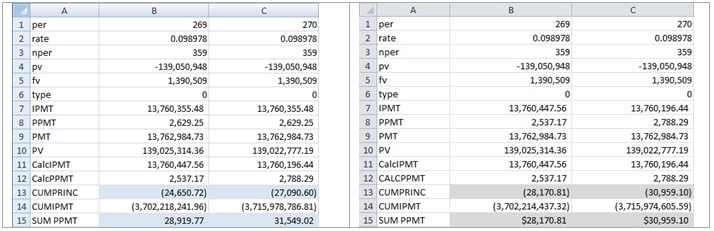
As you can see, in EXCEL 2010 beta, the sum of the PPMT calculations is equal, but opposite in sign, to the CUMPRINC calculation. In EXCEL 2007, there seems to be no relation to the CUMPRINC calculation and the SUM of the PPMT amounts. Why are the signs different? CUMPRINC requires that the pv be greater than zero. I have no idea why that should be a restriction, but we had to multiply the pv by -1 to avoid getting an error. This is a pet peeve of mine, that EXCEL imposes sign restrictions when there is no need to, and flips signs for no apparent reason.
Again, good news for EXCEL 2010 users. Not so good for users of previous versions.
We can use similar logic to check the CUMIPMT function. In cell B16 we enter
=SUM(IPMT(B2,ROW(D1:D269),B3,B4,B5,B6))
and press CTRL+SHIFT+ENTER. And, in cell B17 we enter
=SUM(IPMT(B2,ROW(D1:D270),B3,B4,B5,B6))
and press CTRL+SHIFT+ENTER.
EXCEL 2007 EXCEL 2010 beta
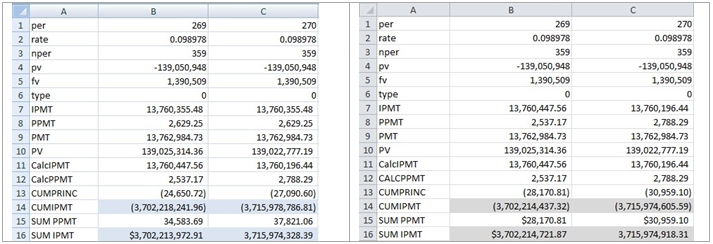
As we expect, at this point, the EXCEL 2007 calculation is off by a few thousand. However, it seems that EXCEL 2010 beta is off by a few hundred. There is another way to check the CUMIPMT calculation. Given the payment (PMT) amount, the number of periods, and the CUMPRINC amount, all of which we have calculated and verified, the CUMIPMT amount is simply the payment amount multiplied by the number of periods minus the cumulative principal amount. In cell B17 enter:
=B9*B1+B21
and copy the B17 to C17.
Here are the results
EXCEL 2007 EXCEL 2010 beta
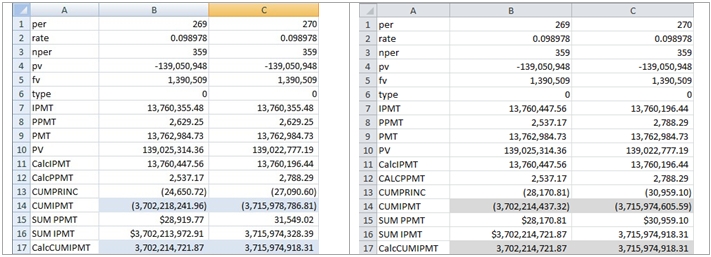
We can see that in row 17, EXCEL 2007 and EXCEL 2010 beta return the same results and that these results agree with the calculation performed in the array formula in EXCEL 2010 beta. It seems safe to conclude that not only is the EXCEL 2007 CUMIPMT function off by a few thousand, but the EXCEL 2010 beta CUMIPMT function is off the by a few hundred.
It seems like it shouldn’t have been too hard to get this calculation right. I guess that this will become part of the improved accuracy for some future release of EXCEL. Or, since EXCEL 2010 is still beta, maybe it will be fixed when it is released for production. In the meantime, I guess we need to get busy checking our existing worksheets.
What is clear in all of this, however, is that EXCEL’s notions of “improved accuracy” may not precisely convey either the scope of the problem or the essence of the solution.