Creating a loan amortization schedule in SQL Server
Feb
2
Written by:
Charles Flock
2/2/2010 6:24 PM

Using the PV, IPMT, PPMT, and PMT functions in XLeratorDB/financial to create a loan amortization schedule in a SELECT statement in SQL Server.
I was reviewing our internal reports showing what keywords are driving traffic to our site and I was struck by how often people were searching for ways to calculate loan amortization in SQL Server. I then reviewed the site and saw that I had written a blog about a year ago about how to use the XLeratorDB functions to create your own table-valued function to do exactly that. But, in looking at that blog, I realized that it makes things seem more complicated than they need to be. By using an auxiliary table of numbers (which is well-documented by Itzik Ben-Gan in Inside Microsoft SQL Server 2005: T-SQL Querying), it is quite straightforward to create the amortization schedule in a SELECT by using the PV, IPMT, PPMT, and PMT functions.
Usually I explain how everything works first, but this time I will present the SQL first, and then I will explain everything at the end. This example is in SQL 2008:
DECLARE @PV as Float = -1000000 --Loan Amount
,@FV as float = 0 --Value of the loan at termination
,@Term as float = 15 --The term of the loan in years
,@Pay_type as bit = 0 --Identifies the payment as due at the end (0) or the
beginning (1) of the period
,@annual_rate as float = .07 --The annual rate of interest
,@payment_frequency as float = 26 --The number of payments in a year
,@rate as float
,@nper as float
Set @rate = @annual_rate/@payment_frequency
Set @nper = @Term * @payment_frequency
;WITH
Nbrs_3( n ) AS ( SELECT 1 UNION SELECT 0 ),
Nbrs_2( n ) AS ( SELECT 1 FROM Nbrs_3 n1 CROSS JOIN Nbrs_3 n2 ),
Nbrs_1( n ) AS ( SELECT 1 FROM Nbrs_2 n1 CROSS JOIN Nbrs_2 n2 ),
Nbrs_0( n ) AS ( SELECT 1 FROM Nbrs_1 n1 CROSS JOIN Nbrs_1 n2 ),
Nbrs ( n ) AS ( SELECT 1 FROM Nbrs_0 n1 CROSS JOIN Nbrs_0 n2 )
SELECT n as [Period]
,-wct.PV(@rate,@nper-(n-1),wct.PMT(@rate,@nper,@PV,@FV,@pay_type),@FV,@pay_type) as [Starting Balance]
,wct.PMT(@rate,@nper,@PV,@FV,@pay_type) as [Payment]
,wct.IPMT(@rate,n,@nper,@PV,@FV,@pay_type) as [Interest Payment]
,wct.PPMT(@rate,n,@nper,@PV,@FV,@pay_type) as [Principal Payment]
,-wct.PV(@rate,@nper-n,wct.PMT(@rate,@nper,@PV,@FV,@pay_type),@FV,@pay_type) as [Ending Balance]
FROM ( SELECT ROW_NUMBER() OVER (ORDER BY n)
FROM Nbrs ) D( n )
WHERE n <= @nper
These are the results from the first 15 lines of the resultant table.
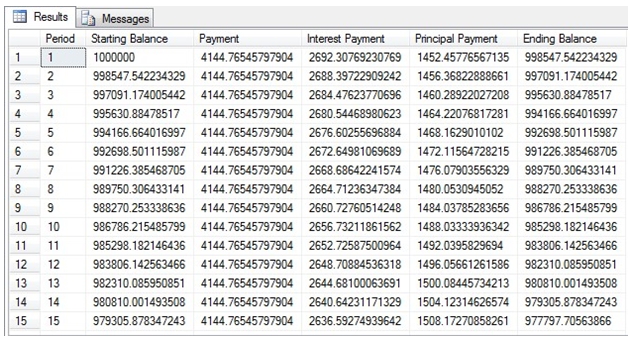
We created an amortization schedule for a 15-year, $1 million loan, at annual interest rate of 7%, with payments every 2 weeks (26 times per year). The SQL can be broken down into 3 parts.
At the beginning, we have created some variables which are passed to the PV, PMT, IPMT, and PPMT functions. This saves us having to type the same information into each of the functions.
DECLARE @PV as Float = -1000000 --Loan Amount
,@FV as float = 0 --Value of the loan at termination
,@Term as float = 15 --The term of the loan in years
,@Pay_type as bit = 0 --Identifies the payment as due at the end (0) or the
beginning (1) of the period
,@annual_rate as float = .07 --The annual rate of interest
,@payment_frequency as float = 26 --The number of payments in a year
,@rate as float
,@nper as float
Set @rate = @annual_rate/@payment_frequency
Set @nper = @Term * @payment_frequency
Next, we create our table of auxiliary numbers as a CTE. This particular implementation will create numbers from 1 to 65536.
;WITH
Nbrs_3( n ) AS ( SELECT 1 UNION SELECT 0 ),
Nbrs_2( n ) AS ( SELECT 1 FROM Nbrs_3 n1 CROSS JOIN Nbrs_3 n2 ),
Nbrs_1( n ) AS ( SELECT 1 FROM Nbrs_2 n1 CROSS JOIN Nbrs_2 n2 ),
Nbrs_0( n ) AS ( SELECT 1 FROM Nbrs_1 n1 CROSS JOIN Nbrs_1 n2 ),
Nbrs ( n ) AS ( SELECT 1 FROM Nbrs_0 n1 CROSS JOIN Nbrs_0 n2 )
Finally, we have the SELECT statement which uses the CTE and the appropriate functions.
SELECT n as [Period]
,-wct.PV(@rate,@nper-(n-1),wct.PMT(@rate,@nper,@PV,@FV,@pay_type),@FV,@pay_type) as [Starting Balance]
,wct.PMT(@rate,@nper,@PV,@FV,@pay_type) as [Payment]
,wct.IPMT(@rate,n,@nper,@PV,@FV,@pay_type) as [Interest Payment]
,wct.PPMT(@rate,n,@nper,@PV,@FV,@pay_type) as [Principal Payment]
,-wct.PV(@rate,@nper-n,wct.PMT(@rate,@nper,@PV,@FV,@pay_type),@FV,@pay_type) as [Ending Balance]
FROM ( SELECT ROW_NUMBER() OVER (ORDER BY n)
FROM Nbrs ) D( n )
WHERE n <= @nper
Since we use the ROW_NUMBER() function to generate the period (n), SQL Server doesn’t bother to generate numbers greater than the value specified by @nper, so there is nothing to worry about in terms of performance.
Our output consists of: the period number, starting balance, payment, interest payment, principal payment, and ending balance.
We have calculated the starting balance as the present value of all the remaining payments multiplied by -1. When we call the PV function, we pass in the number of periods as @nper-(n-1). Thus, the starting balance in the first period is the present value of 390 payments of 4144.76545797904 discounted at a rate of .07/26.0. The starting balance in the 15th period is the present value of 376 payments of 4144.76545797904 discounted at a rate of .07/26.0.
The PMT function calculated the payment amount. It is important to remember that, assuming that the interest rate is greater than zero, the sign on the payment amount is opposite the sign of the principal amount passed into the function.
The IPMT function calculated the interest payment amount. The IPMT value is calculated independently for each period, so the only thing that changes is the value of n passed into the function.
The PPMT function calculated the principal payment amount. Just like IPMT, the value is calculated independently for each period, so as n changes, the PPMT value changes. The PPMT amount will be the difference between the starting balance and the ending balance.
The PV function multiplied by -1 is used again to calculate the ending balance, with the number of periods equal to @nper – n, which is one period less than the number of periods used to calculate the starting balance.
I think that it is actually easier to do this type of calculation in SQL Server than in EXCEL or Reporting Services. By using the auxiliary number table, it is incredibly easy to generate an amortization schedule for almost any type of loan. Whether there are 20 or 2000 amortization periods, we don’t have to make any changes.
One final twist we might want to look at is generating dates as part of the amortization schedule. To do this, I declare another local variable:
@startdate as datetime = '1/21/2010'
I then added the following statement to my SELECT.
SELECT n as [Period]
,CASE @payment_frequency
WHEN 13 THEN convert(varchar, DATEADD(week,4*n,@startdate),106)
WHEN 26 THEN convert(varchar, DATEADD(week,2*n,@startdate),106)
WHEN 52 THEN convert(varchar, DATEADD(week,n,@startdate),106)
ELSE convert(varchar, DATEADD(M,12*n/@payment_frequency,@startdate),106)
END as [Due Date]
If the payment frequency is 13,26,or 52, I increment the start date in mutiples of weeks, otherwise I increment it in multiples of months. I have also used the convert function to reformat the date to make it more readable. Now, the entire script looks like this:
DECLARE @PV as Float = -1000000 --Loan Amount
,@FV as float = 0 --Value of the loan at termination
,@Term as float = 15 --The term of the loan in years
,@Pay_type as bit = 0 --Identifies the payment as due at the end (0) or the
beginning (1) of the period
,@annual_rate as float = .07 --The annual rate of interest
,@payment_frequency as float = 26 --The number of payments in a year
,@startdate as datetime = '1/21/2010'
,@rate as float
,@nper as float
Set @rate = @annual_rate/@payment_frequency
Set @nper = @Term * @payment_frequency
;WITH
Nbrs_3( n ) AS ( SELECT 1 UNION SELECT 0 ),
Nbrs_2( n ) AS ( SELECT 1 FROM Nbrs_3 n1 CROSS JOIN Nbrs_3 n2 ),
Nbrs_1( n ) AS ( SELECT 1 FROM Nbrs_2 n1 CROSS JOIN Nbrs_2 n2 ),
Nbrs_0( n ) AS ( SELECT 1 FROM Nbrs_1 n1 CROSS JOIN Nbrs_1 n2 ),
Nbrs ( n ) AS ( SELECT 1 FROM Nbrs_0 n1 CROSS JOIN Nbrs_0 n2 )
SELECT n as [Period]
,CASE @payment_frequency
WHEN 13 THEN convert(varchar, DATEADD(week,4*n,@startdate),106)
WHEN 26 THEN convert(varchar, DATEADD(week,2*n,@startdate),106)
WHEN 52 THEN convert(varchar, DATEADD(week,n,@startdate),106)
ELSE convert(varchar, DATEADD(M,12*n/@payment_frequency,@startdate),106)
END as [Due Date]
,-wct.PV(@rate,@nper-(n-1),wct.PMT(@rate,@nper,@PV,@FV,@pay_type),@FV,@pay_type) as [Starting Balance]
,wct.PMT(@rate,@nper,@PV,@FV,@pay_type) as [Payment]
,wct.IPMT(@rate,n,@nper,@PV,@FV,@pay_type) as [Interest Payment]
,wct.PPMT(@rate,n,@nper,@PV,@FV,@pay_type) as [Principal Payment]
,-wct.PV(@rate,@nper-n,wct.PMT(@rate,@nper,@PV,@FV,@pay_type),@FV,@pay_type) as [Ending Balance]
FROM ( SELECT ROW_NUMBER() OVER (ORDER BY n)
FROM Nbrs ) D( n )
WHERE n <= @nper
These are the results from the first 15 lines of the resultant table.
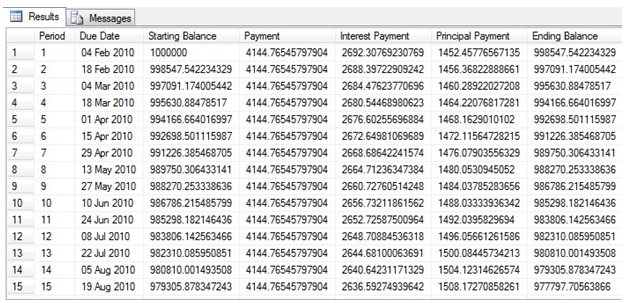
This is a very simple way to generate a loan amortization schedule using T-SQL and a few XLeratorDB functions. Because of this, any device that can establish a connection to the database can execute the SQL. And, if you need the schedule on the database, there is no reason to calculate elsewhere and then add the results to the database. Everything can happen in the database layer.