New Interpolation functions in XLeratorDB
Oct
19
Written by:
Charles Flock
10/19/2009 5:34 PM

A brief description of the new functionality in Math release 1.02
In the new Math release (1.02), we have added functions for linear interpolation (INTERP and INTERP_q) and cubic spline interpolation (SPLINE and SPLINE_q). I have always been somewhat surprised that these functions are not available in EXCEL. They are extremely powerful when used in SQL Server.
Linear interpolation is the simpler of the two methods and, as its name implies, calculates a straight line between the points (xo, y0) and (x1, y1), such that for a given value at x, the value for y is:
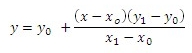
The XLeratorDB linear interpolation function does not require the x- and y-coordinates to be in order; it automatically finds the coordinates surrounding the x-coordinate.
The linear interpolation function does not extrapolate. If the new x-coordinate supplied to the function exceeds the bounds of the x-coordinates passed into the function, the function returns an error. If you want to extrapolate a value along the line that best fits the curve, you can use the XLeratorDB functions TREND or TREND_q.
Cubic spline interpolation is a little harder to explain. Technically, cubic spline interpolation is a form of interpolation where the interpolant is a special type of piecewise polynomial called a spline; not that the definition is very helpful. The way that I think about cubic spline interpolation is that it smoothes the whole curve to calculate the new y-coordinate. Unlike linear interpolation, which only requires the points surrounding the new x-coordinate, the spline interpolates using all the x- and y-coordinates. As a result, the existing x-coordinates are not boundaries for the new x-coordinate. I will avoid giving you the equations involved in doing this calculation, as it is beyond the scope of this blog.
Let’s compare the results of linear interpolation and cubic spline interpolation using the following x- and y-coordinates.
|
X
|
Y
|
|
-3.14159265
|
-1.00
|
|
-1.57079633
|
0.00
|
|
0
|
1.00
|
|
1.57079633
|
0.00
|
|
3.14159265
|
-1.00
|
We can insert these values into a temporary table called xy#:
CREATE TABLE xy# (
[x] [float] NOT NULL,
[y] [float] NOT NULL,
)
INSERT INTO xy# VALUES(-3.14159265358979,-1)
INSERT INTO xy# VALUES(-1.5707963267949,0)
INSERT INTO xy# VALUES(0,1)
INSERT INTO xy# VALUES(1.5707963267949,0)
INSERT INTO xy# VALUES(3.14159265358979,-1)
which you should be able to recognize as the cosine function. We can then write a CTE to create a bunch of new x-coordinate between negative PI and PI, and using those new x-coordinates compare the results between the linear interpolated values and the spline interpolated values and the actual cosiine values.
;with mycte as (
select cast(-3.0 as float) as new_x
union all
select round(new_x + 0.1, 1) as new_x
from mycte
where new_x < 3.0
) select new_x
,wct.INTERP('xy#','x','y','',NULL,new_x) as Linear
,wct.SPLINE('xy#','x','y','',NULL,new_x) as Spline
,cos(new_x) as [Cosine(x)]
from mycte
This produces the following results:
new_x Linear Spline Cosine(x)
---------------------- ---------------------- ---------------------- ----------------------
-3 -0.909859317102746 -0.922631925525076 -0.989992496600445
-2.9 -0.846197339865987 -0.867649399649816 -0.970958165149591
-2.8 -0.782535362629229 -0.812132583457798 -0.942222340668658
-2.7 -0.718873385392471 -0.755860323570052 -0.904072142017061
-2.6 -0.655211408155712 -0.698611466607605 -0.856888753368947
-2.5 -0.591549430918954 -0.640164859191489 -0.801143615546934
-2.4 -0.527887453682195 -0.580299347942733 -0.737393715541245
-2.3 -0.464225476445437 -0.518793779482365 -0.666276021279824
-2.2 -0.400563499208679 -0.455427000431417 -0.588501117255346
-2.1 -0.33690152197192 -0.389977857410916 -0.504846104599858
-2 -0.273239544735162 -0.322225197041893 -0.416146836547142
-1.9 -0.209577567498403 -0.251947865945377 -0.323289566863503
-1.8 -0.145915590261645 -0.178924710742398 -0.227202094693087
-1.7 -0.0822536130248864 -0.102934578053985 -0.128844494295525
-1.6 -0.0185916357881281 -0.0237563145011674 -0.0291995223012888
-1.5 0.0450703414486301 0.0587527593013531 0.0707372016677029
-1.4 0.108732318685388 0.143947351759551 0.169967142900241
-1.3 0.172394295922146 0.230727204131879 0.267498828624587
-1.2 0.236056273158904 0.317986549523483 0.362357754476674
-1.1 0.299718250395662 0.404619621039511 0.453596121425577
-1 0.36338022763242 0.489520651785112 0.54030230586814
-0.9 0.427042204869178 0.571583874865431 0.621609968270664
-0.8 0.490704182105936 0.649703523385617 0.696706709347165
-0.7 0.554366159342694 0.722773830450817 0.764842187284489
-0.6 0.618028136579452 0.789689029166179 0.825335614909678
-0.5 0.68169011381621 0.84934335263685 0.877582561890373
-0.4 0.745352091052968 0.900631033967977 0.921060994002885
-0.3 0.809014068289726 0.942446306264708 0.955336489125606
-0.2 0.872676045526484 0.973683402632191 0.980066577841242
-0.1 0.936338022763242 0.993236556175572 0.995004165278026
0 1 1 1
0.1 0.936338022763242 0.993236556175572 0.995004165278026
0.2 0.872676045526484 0.973683402632191 0.980066577841242
0.3 0.809014068289726 0.942446306264708 0.955336489125606
0.4 0.745352091052968 0.900631033967977 0.921060994002885
0.5 0.68169011381621 0.84934335263685 0.877582561890373
0.6 0.618028136579452 0.789689029166179 0.825335614909678
0.7 0.554366159342694 0.722773830450817 0.764842187284489
0.8 0.490704182105936 0.649703523385617 0.696706709347165
0.9 0.427042204869178 0.571583874865431 0.621609968270664
1 0.36338022763242 0.489520651785112 0.54030230586814
1.1 0.299718250395662 0.404619621039511 0.453596121425577
1.2 0.236056273158904 0.317986549523483 0.362357754476674
1.3 0.172394295922146 0.230727204131879 0.267498828624587
1.4 0.108732318685388 0.143947351759551 0.169967142900241
1.5 0.0450703414486301 0.0587527593013531 0.0707372016677029
1.6 -0.0185916357881281 -0.0237563145011674 -0.0291995223012888
1.7 -0.0822536130248864 -0.102934578053985 -0.128844494295525
1.8 -0.145915590261645 -0.178924710742398 -0.227202094693087
1.9 -0.209577567498403 -0.251947865945377 -0.323289566863503
2 -0.273239544735162 -0.322225197041893 -0.416146836547142
2.1 -0.33690152197192 -0.389977857410916 -0.504846104599858
2.2 -0.400563499208679 -0.455427000431417 -0.588501117255346
2.3 -0.464225476445437 -0.518793779482365 -0.666276021279824
2.4 -0.527887453682195 -0.580299347942733 -0.737393715541245
2.5 -0.591549430918954 -0.640164859191489 -0.801143615546934
2.6 -0.655211408155712 -0.698611466607605 -0.856888753368947
2.7 -0.718873385392471 -0.755860323570052 -0.904072142017061
2.8 -0.782535362629229 -0.812132583457798 -0.942222340668658
2.9 -0.846197339865987 -0.867649399649816 -0.970958165149591
3 -0.909859317102746 -0.922631925525076 -0.989992496600445
(61 row(s) affected)
As you can see, for this type of function, spline almost always gives a better result than linear interpolation.
Let’s look at another example, using US Census data.
|
X
|
Y
|
|
1900
|
76212168
|
|
1910
|
92228496
|
|
1920
|
106021537
|
|
1930
|
123202624
|
|
1940
|
132164569
|
|
1950
|
151325798
|
|
1960
|
179323175
|
|
1970
|
203211926
|
|
1980
|
226545805
|
|
1990
|
248709873
|
|
2000
|
281421906
|
Again, we will use a temporary table called xy#:
CREATE TABLE xy# (
[x] [float] NOT NULL,
[y] [float] NOT NULL,
)
INSERT INTO xy# VALUES(1900,76212168)
INSERT INTO xy# VALUES(1910,92228496)
INSERT INTO xy# VALUES(1920,106021537)
INSERT INTO xy# VALUES(1930,123202624)
INSERT INTO xy# VALUES(1940,132164569)
INSERT INTO xy# VALUES(1950,151325798)
INSERT INTO xy# VALUES(1960,179323175)
INSERT INTO xy# VALUES(1970,203211926)
INSERT INTO xy# VALUES(1980,226545805)
INSERT INTO xy# VALUES(1990,248709873)
INSERT INTO xy# VALUES(2000,281421906)
Since Census data are only available decennially, you can only estimate the population for intervening years. If we wanted to estimate the population for 1995, we could enter the following statement:
select wct.INTERP('xy#','x','y','',NULL,1995) as Linear
,wct.SPLINE('xy#','x','y','',NULL,1995) as Spline
This returns the following estimate:
Linear Spline
---------------------- ----------------------
265065889.5 263967768.44222
One interesting thing that we can do with the SPLINE function, is estimate the population for 2010. We cannot do this using the INTERP function, as INTERP requires that the existing x-coordinates bound the new x-coordinate. To calculate the 2010 population, using the historical census data, we enter the following statement:
select wct.SPLINE('xy#','x','y','',NULL,2010) as [2010 Estimate]
This returns the following estimate:
2010 Estimate
----------------------
314133939
How does this compare with the TREND and GROWTH functions? The following SELECT statements tell us:
select wct.SPLINE('xy#','x','y','',NULL,2010) as [2010 Spline Estimate]
,wct.TREND('xy#','y','x','',NULL,2010) as [2010 Trend Estimate]
,wct.GROWTH('xy#','y','x','',NULL,2010) as [2010 Growth Estimate]
This returns the following estimate:
2010 Spline Estimate 2010 Trend Estimate 2010 Growth Estimate
---------------------- ---------------------- ----------------------
314133939 286618400.381818 329443554.337062
The SPLINE calculation is about 28 million more than the TREND calculation and about 15 million less than the GROWTH calculation. Since the US population is widely estimated to be above 300 million already, it would seem that the TREND estimate has underestimated the population growth. We won’t really know for sure until after the Census, but my guess would be that the SPLINE estimate of the population will be closer to the actual number than the GROWTH estimate.