New t-Test functions in XLeratorDB/statistics 1.11
Jul
18
Written by:
Charles Flock
7/18/2012 4:56 PM
We have a new functionality for the t-Test allowing you to perform sophisticated analysis of your SQL Server data directly on the database using TSQL.
In release 1.11 we have added three new functions for the t-Test: TTEST_PAIRED (the paired t-Test), TTEST_INDEP (the two-sample t-Test assuming equal variance), and TTEST_INDEPU (the two-ample t-Test assuming unequal variance). In addition to calculating the t-Test p-value (which was already available in the existing TTEST function), you can now get other test characteristics, including the test statistic, the degrees of freedom, the pooled variance, and the effect size.
It is possible to get some of this information out of EXCEL, but there are no EXCEL functions that will provide anything other than the p-value. You need to use the Data Analysis features of EXCEL to get anything other than the p-value.
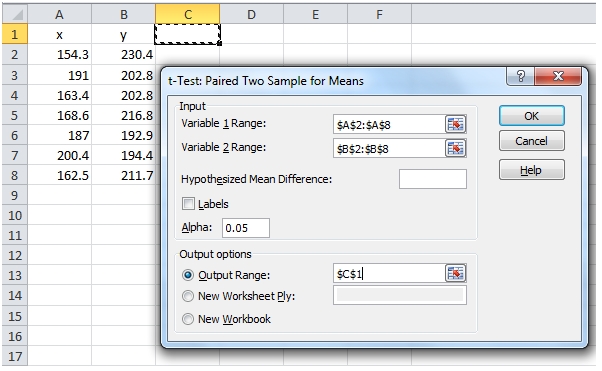
Here’s an example of the paired t-Test in EXCEL using Data Analysis.
|
t-Test: Paired Two Sample for Means
|
|
|
|
|
|
|
Variable 1
|
Variable 2
|
|
Mean
|
175.3142857
|
207.4
|
|
Variance
|
300.7880952
|
176.2366667
|
|
Observations
|
7
|
7
|
|
Pearson Correlation
|
-0.806734967
|
|
|
Hypothesized Mean Difference
|
0
|
|
|
df
|
6
|
|
|
t Stat
|
-2.914289804
|
|
|
P(T<=t) one-tail
|
0.013415026
|
|
|
t Critical one-tail
|
1.943180281
|
|
|
P(T<=t) two-tail
|
0.026830053
|
|
|
t Critical two-tail
|
2.446911851
|
|
Notice that there is no effect size returned in the EXCEL table, and there is no way to calculate the effect size from the table values. Additionally, if the data change, then Data Analysis needs to be re-run, so it’s quite easy for the table and the results to get out of synch. This made EXCEL pretty much unsuitable as a testing platform.
EXCEL also produces results for something called P(T<=t) one-tail and P(T<=t) two-tail. These values are simply TINV(2*alpha, df) and TINV(alpha, df), respectively. Take note that this is TINV function and not the T.INV function in EXCEL 2010. Using T.INV, the formula would be T.INV(1-alpha,df) and T.INV((1-alpha)/2,df), respectively.
However, even knowing how the values are calculated doesn’t really tell us what the description means. None of the other applications that we looked at produced this value. If you need to produce this value, you can use the XLeratorDB TINV function to do the calculation.
This led us to use MATLAB and R for testing purposes. We tested against the ttest and ttest2 functions in MATLAB and the t.test function in R.
In R, you can just paste the following into the R console:
x<-c(154.3,191,163.4,168.6,187,200.4,162.5)
y<-c(230.4,202.8,202.8,216.8,192.9,194.4,211.7)
t.test(x,y,paired = TRUE)
and it will produce the following result.
Paired t-test
data: x and y
t = -2.9143, df = 6, p-value = 0.02683
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-59.025696 -5.145732
sample estimates:
mean of the differences
-32.0857
You can see that R also does not report on effect size, but does include upper and lower confidence levels.
In MATLAB, paste this into the Command Window:
x=[154.3,191,163.4,168.6,187,200.4,162.5];
y=[230.4,202.8,202.8,216.8,192.9,194.4,211.7];
[h,p,ci,stats] = ttest(x,y)
And the following values are returned.
h = 1
p = 0.026830052564695
ci = -59.025696174081908 -5.145732397346670
stats =
tstat: -2.914289804035312
df: 6
sd: 29.129162281776917
Like R, MATLAB does not calculate the effect size, but does include the confidence interval. It also includes an sd statistic, which is the standard deviation of the differences.
In SQL Server using XLeratorDB, we can enter the following into SQL Server Management Studio.
SELECT t.s
,t.descr
,wct.TTEST_PAIRED(x,y,t.s) as [Value]
FROM (VALUES
(154.3,230.4),
(191,202.8),
(163.4,202.8),
(168.6,216.8),
(187,192.9),
(200.4,194.4),
(162.5,211.7)
) n(x,y)
CROSS APPLY(VALUES
('P1','one tailed p_value'),
('P2','two tailed p_value'),
('T','t observed'),
('ES','effect size'),
('N','num observed'),
('DF','deg freedom'),
('MD','mean difference'),
('SDD','stdev difference'),
('SE','standard error'),
('R','Pearsons correlation'),
('LCL','lower confidence level'),
('UCL','upper confidence level')
)t(s,descr)
GROUP BY t.s, t.descr
This produces the following results.
s descr Value
---- ---------------------- ----------------------
P1 one tailed p_value 0.0134150262823471
P2 two tailed p_value 0.0268300525646943
T t observed -2.91428980403532
ES effect size -1.10149800997837
N num observed 7
DF deg freedom 6
MD mean difference -32.0857142857143
SDD stdev difference 29.1291622817769
SE standard error 11.0097884710321
R Pearsons correlation -0.806734967138168
LCL lower confidence level -59.025696174082
UCL upper confidence level -5.14573239734668
As you can see, XLeratorDB includes a variety of descriptive statistics about the paired t-Test, which matches up to the results produced by EXCEL, R, and MATLAB.
However, we had to check the effect size calculations arithmetically. For this we used Summary of Effect Sizes and their Links to Inferential Statistics by Michael Furr published in March 2008. For the paired t-Test, the effect size is calculated as Cohen’s d, using the Furr 1.2.3:
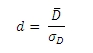
Where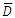 
is the mean difference and sD is the standard deviation of the difference scores. Financial users will immediately recognize this equation as the Sharpe ratio. This makes it possible to use the TTEST_PAIRED function to calculate the Sharpe Ratio in a very straightforward way. Here’s an example with monthly portfolio returns and a risk-free rate of .05 per month.
SELECT wct.TTEST_PAIRED(r,.05,'ES') as Sharpe
FROM (VALUES
(1,0.259),(2,0.198),(3,0.364),(4,-0.081),(5,0.057),(6,0.055),
(7,0.188),(8,0.317),(9,0.240),(10,0.184),(11,-0.01),(12,0.526)
) n(per,r)
This produces the following result.
Sharpe
----------------------
0.834363920967124
The paired t-Test requires a pair of values. If either of the values is NULL, the pair is not included in the calculations. If you went to perform a t-Test against a hypothetical mean, simply enter the hypothetical mean as the y-value instead of a column name. If you want to test the x-values against the standard normal distribution, simply enter 0 as the y-value. If you want to perform a paired t-Test against a hypothetical mean, you can simple add the hypothetical mean to the y-value in the SQL. For example, this calculation returns the values for a paired t-Test where the hypothetical mean is 20.
SELECT wct.TTEST_PAIRED(control, treatment+20, 'T') as t_observed
,wct.TTEST_PAIRED(control, treatment+20, 'P1') as p1_value
,wct.TTEST_PAIRED(control, treatment+20, 'P2') as p2_value
,wct.TTEST_PAIRED(control, treatment+20, 'R') as PCC
,wct.TTEST_PAIRED(control, treatment+20, 'LCL') as lower_ci
,wct.TTEST_PAIRED(control, treatment+20, 'UCL') as upper_ci
FROM (VALUES
(237,194),
(289,240),
(257,230),
(228,186),
(303,265),
(275,222),
(262,242),
(304,281),
(244,240),
(233,212)) n(control,treatment)
This produces the following result.
|
t_observed
|
p1_value
|
p2_value
|
PCC
|
lower_ci
|
upper_ci
|
|
2.459760185
|
0.018086
|
0.036173
|
0.85834
|
0.964011
|
23.03599
|
Not only does the XLeratorDB function calculate a wide variety of descriptive statistics associated with the paired t-Test, but since it is an object on the database, it can consume massive amounts of data very quickly, without having to transport the x-values and y-values over the network. In our test environment, a 2.5gHz Dual Core Pentium machine running SQL Server 2008 R2 with 4GB RAM running Windows Server 2008 we processed over 30,000 rows/second, with each row containing a paired x- and y-value.
Now, let’s look at the two-sample t-Test for independent means assuming equal variance.
Let’s say we had the following values that we wanted to perform the two-sample t-Test for independent means assuming equal variance
|
x
|
Y
|
|
165.9
|
212.1
|
|
210.3
|
203.5
|
|
166.8
|
210.3
|
|
182.3
|
228.4
|
|
182.1
|
206.2
|
|
218
|
203.2
|
|
170.1
|
224.9
|
|
|
202.6
|
In EXCEL we could simply put these values in columns A and B then using the Data Analysis tool, select the appropriate t-Test and put the results in C1.
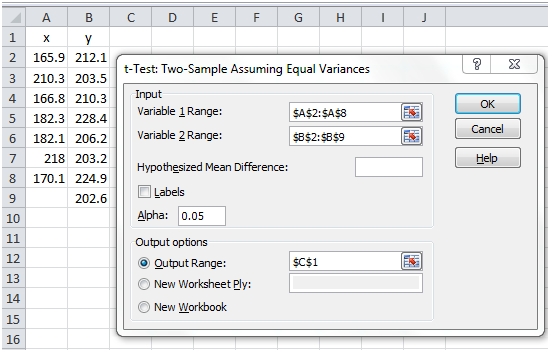
This produces the following output
|
t-Test: Two-Sample Assuming Equal Variances
|
|
|
|
|
|
|
|
|
Variable 1
|
Variable 2
|
|
Mean
|
185.0714286
|
211.4
|
|
Variance
|
443.802381
|
101.0114286
|
|
Observations
|
7
|
8
|
|
Pooled Variance
|
259.2226374
|
|
|
Hypothesized Mean Difference
|
0
|
|
|
df
|
13
|
|
|
t Stat
|
-3.159651739
|
|
|
P(T<=t) one-tail
|
0.0037652
|
|
|
t Critical one-tail
|
1.770933396
|
|
|
P(T<=t) two-tail
|
0.0075304
|
|
|
t Critical two-tail
|
2.160368656
|
|
Again, there is no calculation of the effect size. It’s also important to note that the x- and y-values are no longer treated as pairs. Additionally, there is another value produced by EXCEL, called the Pooled Variance.
In R, you can just paste the following into the R console:
x<-c(165.9,210.3,166.8,182.3,182.1,218.0,170.1)
y<-c(212.1,203.5,210.3,228.4,206.2,203.2,224.9,202.6)
t.test(x,y,var.equal = TRUE)
This produces the following result.
Two Sample t-test
data: x and y
t = -3.1597, df = 13, p-value = 0.00753
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-44.330372 -8.326771
sample estimates:
mean of x mean of y
185.0714 211.4000
In MATLAB, paste this into the Command Window:
x=[165.9,210.3,166.8,182.3,182.1,218.0,170.1];
y=[212.1,203.5,210.3,228.4,206.2,203.2,224.9,202.6];
[h,p,ci,stats] = ttest2(x,y)
This produces the following result.
h = 1
p = 0.007530400275588
ci = -44.330372000894251 -8.326770856248594
stats =
tstat: -3.159651739014238
df: 13
sd: 16.100392459894802
Again, neither R nor MATLAB produce the effect size, though both produce confidence intervals which are not produced by EXCEL. R does not provide a figure for the Pooled Variance and MATLAB produces a statistic labeled sd, which is equal to the square root of the pooled variance (which I guess makes it the pooled standard deviation).
Unlike the paired t-Test, the t-Test for independent means does not require that the number of x-values equal the number of y-values. In EXCEL and the other tools, x and y are treated as vectors and passed into the functions as vectors of unequal length. There is no vector data structure in SQL Server, and we can’t just pass in x and y as column names, since they can be of different lengths.
Supporting vectors of unequal length in SQL Server is quite achievable, provided that your data are properly normalized. Instead of thinking about a vector of x-values and a vector of y-values, we need to think about a set of data which contains test results and labels which identify the results as belonging to the x-sample or the y-sample. Of course, the labels do not have to be ‘x’ or ‘y’; they can be anything that you like. The important thing is that each test calculation must consist of exactly two labels and you must identify which of the two labels is the ‘x’ (or left-side) of the test. This is important as it will determine the sign on the t-statistic.
Using the same data as above in XLeratorDB you can paste this into SQL Server Management Studio.
SELECT t.s
,t.descr
,wct.TTEST_INDEP(l,val,t.s,'x') as Value
FROM (VALUES
('x',165.9), ('y',212.1),
('x',210.3), ('y',203.5),
('x',166.8), ('y',210.3),
('x',182.3), ('y',228.4),
('x',182.1), ('y',206.2),
('x',218), ('y',203.2),
('x',170.1), ('y',224.9),
('y',202.6)
) n(l,val)
CROSS APPLY(VALUES
('P1','one tailed p-value'),
('P2','two tailed_p-value'),
('T','t observed'),
('ES','effect size'),
('N1','num observed in sample one'),
('N2','num observed in sample two'),
('SD','pooled variance'),
('DF','deg freedom'),
('MD','mean difference'),
('SE','standard error'),
('LCL','lower confidence level'),
('UCL','upper confidence level')
)t(s,descr)
GROUP BY t.s, t.descr
This produces the following result
s descr Value
---- -------------------------- ----------------------
P1 one tailed p-value 0.00376520013779435
P2 two tailed_p-value 0.00753040027558871
T t observed -3.15965173901421
ES effect size -1.63527513345741
N1 num observed in sample one 7
N2 num observed in sample two 8
SD pooled variance 259.222637362642
DF deg freedom 13
MD mean difference -26.3285714285714
SE standard error 8.33274474635162
LCL lower confidence level -44.3303720008945
UCL upper confidence level -8.32677085624837
For TTEST_INDEP, the effect size is calculated as
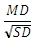
For more information, see Furr 1.2.1
As with the paired t-Test, the XLeratorDB function TTEST_INDEP calculates a wide variety of descriptive statistics associated with the two-sample t-Test for independent means assuming equal variance, Again, since it is an object on the database, it can consume massive amounts of data very quickly, without having to transport the x-values and y-values over the network. In our test environment, a 2.5gHz Dual Core Pentium machine running SQL Server 2008 R2 with 4GB RAM running Windows Server 2008 we processed over 50,000 rows/second, with each row containing a single x-value or a single y-value.
Finally, let’s look at the two-sample t Test assuming Unequal Variances
This produces the following output
|
t-Test: Two-Sample Assuming Unequal Variances
|
|
|
|
|
|
|
Variable 1
|
Variable 2
|
|
Mean
|
185.0714286
|
211.4
|
|
Variance
|
443.802381
|
101.0114286
|
|
Observations
|
7
|
8
|
|
Hypothesized Mean Difference
|
0
|
|
|
df
|
8
|
|
|
t Stat
|
-3.01956254
|
|
|
P(T<=t) one-tail
|
0.008285256
|
|
|
t Critical one-tail
|
1.859548038
|
|
|
P(T<=t) two-tail
|
0.016570512
|
|
|
t Critical two-tail
|
2.306004135
|
|
Again, there is no calculation of the effect size. Unlike two-sample t-Test assuming equal variance, there is no Pooled Variance. Also, EXCEL, unlike R and MATLAB, calculates the degrees of freedom as an integer, which is not what happens in the EXCEL TTEST function. This leads to the problem that the numbers produced by Data Analysis in EXCEL do not agree with the numbers produced by the TTEST function in EXCEL. I have no idea why EXCEL would choose to do this, other than the T.DIST function, which can be used to calculated the p-value in EXCEL, truncates degrees of freedom if it is not an integer. However, the p-value can also be calculated using the BETA.DIST function, which accepts non-integer values. In our implementation, we calculate the degrees of freedom as a floating point value, rather than exclusively as an integer, keeping TTEST_INDEPU consistent with R, MATLAB, and SPSS.
In R, you can just paste the following into the R console:
x<-c(165.9,210.3,166.8,182.3,182.1,218.0,170.1)
y<-c(212.1,203.5,210.3,228.4,206.2,203.2,224.9,202.6)
t.test(x,y)
This produces the following result.
Welch Two Sample t-test
data: x and y
t = -3.0196, df = 8.344, p-value = 0.01579
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-46.291950 -6.365193
sample estimates:
mean of x mean of y
185.0714 211.4000
In MATLAB, paste this into the Command Window:
x=[165.9,210.3,166.8,182.3,182.1,218.0,170.1];
y=[212.1,203.5,210.3,228.4,206.2,203.2,224.9,202.6];
[h,p,ci,stats] = ttest2(x,y,.05,'both','unequal')
This produces the following result.
h = 1
p = 0.015785485650734
ci = -46.291949510052831 -6.365193347090017
stats =
tstat: -3.019562539931532
df: 8.344151362650967
sd: [21.066617691323422 10.050444197717267]
Using the same data as above in XLeratorDB you can paste this into SQL Server Management Studio.
SELECT t.s
,t.descr
,wct.TTEST_INDEPU(l,val,t.s,'x') as Value
FROM (VALUES
('x',165.9), ('y',212.1),
('x',210.3), ('y',203.5),
('x',166.8), ('y',210.3),
('x',182.3), ('y',228.4),
('x',182.1), ('y',206.2),
('x',218), ('y',203.2),
('x',170.1), ('y',224.9),
('y',202.6)
) n(l,val)
CROSS APPLY(VALUES
('P1','one tailed p-value'),
('P2','two tailed_p-value'),
('T','t observed'),
('ES','effect size'),
('N1','num observed in sample one'),
('N2','num observed in sample two'),
('DF','deg freedom'),
('MD','mean difference'),
('SE','standard error'),
('LCL','lower confidence level'),
('UCL','upper confidence level')
)t(s,descr)
GROUP BY t.s, t.descr
This produces the following result.
s descr Value
---- -------------------------- ----------------------
P1 one tailed p-value 0.00789274282536726
P2 two tailed_p-value 0.0157854856507345
T t observed -3.01956253993151
ES effect size -1.63527513345741
N1 num observed in sample one 7
N2 num observed in sample two 8
DF deg freedom 8.34415136265098
MD mean difference -26.3285714285714
SE standard error 8.71933304258326
LCL lower confidence level -46.291949510053
UCL upper confidence level -6.36519334708986
For TTEST_INDEPU, the effect size is calculated as
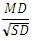
For more information, see Furr 1.2.1
As with the paired t-Test, the XLeratorDB function TTEST_INDEPU calculates a wide variety of descriptive statistics associated with the two-sample t-Test for independent means assuming equal variance, Again, since it is an object on the database, it can consume massive amounts of data very quickly, without having to transport the x-values and y-values over the network. In our test environment, a 2.5gHz Dual Core Pentium machine running SQL Server 2008 R2 with 4GB RAM running Windows Server 2008 we processed over 50,000 rows/second, with each row containing a single x-value or a single y-value, which is pretty much the same as TTEST_INDEP.
We think that the new t-Test functions are a powerful addition to XLeratorDB, allowing users to perform sophisticated statistical calculations right on the database, without having to extract, move, or link their data to any other platform. Let us know what you think.