Correctly calculate the price of a bond with an odd long first period
Oct
18
Written by:
Charles Flock
10/18/2011 8:12 PM

11 Financial Calculations that you can’t do in EXCEL - Part 6 of 11
6. Correctly calculate the price of a bond with an odd long first period
Enter the following data into a worksheet.
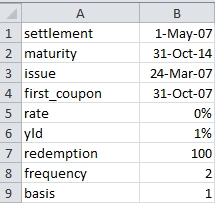
Enter the following formula in B10: =ODDFPRICE(B1,B2,B3,B4,B5,B6,B7,B8,B9)
This produces the following result.
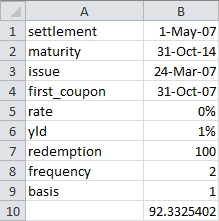
In this example, we have kept things very simple. The rate is zero, so the interest amount included in the calculation is zero. This bond has a long first coupon, with a quasi-coupon data on the 30th of April, 2007 and a first coupon on the 31st of October, 2007.
Since the settlement date is after the quasi-coupon date and since the rate is zero, then the PRICE function should return exactly the same answer as the ODDFPRICE function (for a more detailed explanation of the mechanics of this, you can read this article).
Enter the following formula in B11: =PRICE(B1,B2,B5,B6,B7,B8,B9)
This produces the following result.
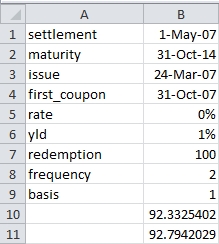
Quite clearly, the PRICE calculation and the ODDFPRICE calculation disagree, even though they use the same inputs and there is only one cash flow, the redemption amount.
Since we are using a zero-coupon bond, it is actually quite easy to see what the problem is. Enter the following formulae in the following cells:
C10 =LOG(B7/B10)/LOG(1+B6/B8)
C11 =LOG(B7/B11)/LOG(1+B6/B8)
D10 =((1+B6/B8)^-C10)*B7
D11 =((1+B6/B8)^-C11)*B7
This produces the following result.
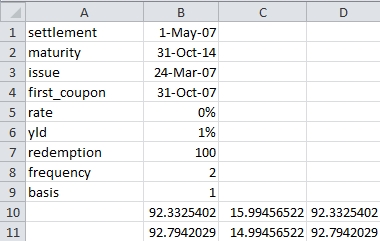
We have used EXCEL to tell us what value ODDFPRICE and PRICE used in determining the number of whole coupon plus the fractional coupon period until maturity and then double-checked that result. As you can see, they disagree by exactly one full coupon period. They can’t both be right.
Here’s what we get in SQL Server.
SELECT wct.ODDFPRICE(
'5/1/2007' --settlement
,'10/31/2014' --maturity
,'3/24/2007' --issue
,'10/31/2007' --first_coupon
,0.00 --rate
,.01 --yld
,100 --redemption
,2 --frequency
,1 --basis
)
This produces the following result
----------------------
92.7942029404091
(1 row(s) affected)