SQL Server Matrix Functions
Jan
21
Written by:
Charles Flock
1/21/2010 8:50 PM

With the latest release of XLeratorDB/math, we add functions for calculation of the matrix product, the matrix determinant, and the matrix inverse.
In XLeratorDB/math release 1.03, we have added 12 new functions supporting matrix math. These functions are the equivalent of the MMULT, MDETERM, and MINVERSE functions in EXCEL.
Generally, we use the terms array and matrix interchangeably. Multiply two matrices, 'A' and 'B', and the result is a third matrix that we can call 'AB'. The 'AB' matrix will have the same number of rows as the 'A' matrix and the same number of columns as the 'B' matrix. In EXCEL, this is straightforward: the 'A' and the 'B' matrices are both ranges that are physically dimensioned by rows and columns. Here is a simple example in EXCEL:
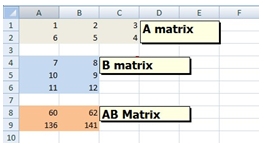
The A matrix is in the range A1:C2; the B matrix is in the range A4:B6. The matrix product AB is in the range A8:B9.
Astute SQL Server users will immediately point out that this data is not in 3rd normal form and that the proper way to represent a matrix on the data base is to have a table where row and column co-ordinates are columns in the table with yet another column holding the value. Something that might look like this:
CREATE TABLE #matrix (
MatrixID varchar(5),
rowno int,
colno int,
val float
)
The advantage to normalizing the table in this manner is that we are no longer sensitive to the dimensions of the matrix. We can use the same data structure whether the matrix is 10 columns or 10,000 columns. It is also minimizes the amount of space required to store the matrix.
To accommodate both normalized and de-normalized arrangements of data we created two versions of the functions. In the case of matrix multiplication, the function for de-normalized data is MMULT and the function for normalized data is MMULTN. We simply added an ‘N’ to the end of the function name to identify that version of the function as being for normalized data. Therefore, there is an MINVERSE and MINVERSEN, an MDETERM and an MDETERMN.
Like all of our ‘range query’ functions there is a simple version, which is meant to be used with a table or view and keeps the SQL very simple and there is a more flexible version which allows you to specify the data to be passed to the function through the use of standard SQL statements. These more flexible versions of the functions have the same function name with ‘_q’ appended to the name. This gives use four function names for each function name in EXCEL. For matrix multiplication, for example, we end up with MMULT, MMULTN, MMULT_q, and MMULTN_q.
Let’s look at what that means. Look at the data that is in our EXCEL spreadsheet. The simplest way to reproduce that calculation in SQL Server is to use the MMULT_q function by entering the following statement:
SELECT *
FROM wct.MMULT_q(
--A matrix ------------
'SELECT 1,2,3 UNION ALL
SELECT 6,5,4',
--B matrix ------------
'SELECT 7,8 UNION ALL
SELECT 10,9 UNION ALL
SELECT 11,12'
)
Producing the following result.
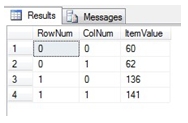
There are a couple of things to notice here. First, the MMULT_q function returns a TABLE instead of a single value. It is a table-valued function and these functions are the first table-valued functions in XLeratorDB. Second, the table that is returned is always in 3rd normal form and has the following definition:
TABLE (
[RowNum] [int] NULL,
[ColNum] [int] NULL,
[ItemValue] [float] NULL)
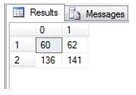
We use this table structure in all of the table-valued functions in this release. If you want to see the results in de-normalized form, you can use the existing T-SQL PIVOT function to do so.
SELECT [0],[1]
FROM (
SELECT *
FROM wct.MMULT_q(
--A Matrix ------------
'SELECT 1,2,3 UNION ALL
SELECT 6,5,4',
--B Matrix ------------
'SELECT 7,8 UNION ALL
SELECT 10,9 UNION ALL
SELECT 11,12'
)) M PIVOT (
MAX(ItemValue)
FOR colnum IN ([0],[1])
) AS pvt
Producing the following result.
Let’s see what this would look like if the data were in a normalized table. Using the #matrix table we created above, let’s insert the data:
INSERT INTO #matrix
SELECT 'A',0,0,1 UNION ALL
SELECT 'A',0,1,2 UNION ALL
SELECT 'A',0,2,3 UNION ALL
SELECT 'A',1,0,6 UNION ALL
SELECT 'A',1,1,5 UNION ALL
SELECT 'A',1,2,4 UNION ALL
SELECT 'B',0,0,7 UNION ALL
SELECT 'B',0,1,8 UNION ALL
SELECT 'B',1,0,10 UNION ALL
SELECT 'B',1,1,9 UNION ALL
SELECT 'B',2,0,11 UNION ALL
SELECT 'B',2,1,12
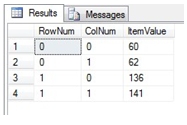
We can use the MMULTN function to calculate the matrix product.
SELECT *
FROM wct.MMULTN(
--A Matrix --
'#matrix'
,'rowno'
,'colno'
,'val'
,'MatrixID'
,'A'
--B Matrix --
,'#matrix'
,'rowno'
,'colno'
,'val'
,'MatrixID'
,'B'
)
This produces the following result.
Even though we have entered our matrices as zero-based, this is not a requirement. The first element in the array can be zero, one, or any number that we choose. For example, we could have entered the matrix as:
INSERT INTO #matrix
SELECT 'A',0,100,1 UNION ALL
SELECT 'A',0,101,2 UNION ALL
SELECT 'A',0,102,3 UNION ALL
SELECT 'A',1,100,6 UNION ALL
SELECT 'A',1,101,5 UNION ALL
SELECT 'A',1,102,4 UNION ALL
SELECT 'B',0,100,7 UNION ALL
SELECT 'B',0,101,8 UNION ALL
SELECT 'B',1,100,10 UNION ALL
SELECT 'B',1,101,9 UNION ALL
SELECT 'B',2,100,11 UNION ALL
SELECT 'B',2,101,12
or even as:
INSERT INTO #matrix
SELECT 'A',0,-2,1 UNION ALL
SELECT 'A',0,-1,2 UNION ALL
SELECT 'A',0,0,3 UNION ALL
SELECT 'A',1,-2,6 UNION ALL
SELECT 'A',1,-1,5 UNION ALL
SELECT 'A',1,0,4 UNION ALL
SELECT 'B',0,-1,7 UNION ALL
SELECT 'B',0,0,8 UNION ALL
SELECT 'B',1,-1,10 UNION ALL
SELECT 'B',1,0,9 UNION ALL
SELECT 'B',2,-1,11 UNION ALL
SELECT 'B',2,0,12
and we would get the same result.
The matrix inverse functions take a single matrix, 'A', as input and return a matrix, 'B', such that the matrix product, 'AB', is equal to the identity matrix, 'I'. The 'A' matrix must be a square matrix, meaning that the number of rows is equal to the number of columns. The returned 'B' matrix has the same number of rows and columns as 'A'. The identity matrix is a square matrix where all the of the matrix values are zero, except where the row number is equal to the column number, in which case the value is one. In other words, all the matrix values are zero, expect the diagonals, which are one.
Here’s how it looks in EXCEL.
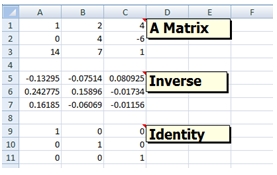
Since the EXCEL data are not in 3rd normal form, we will use the MINVERSE_q function to do the calculation:
SELECT *
FROM wct.MINVERSE_q(
'SELECT 1,2,4 UNION ALL
SELECT 0,4,-6 UNION ALL
SELECT 14,7,1'
)
This produces the following result.
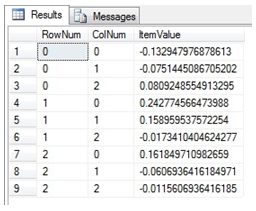
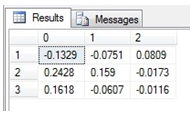
Of course, we can always use the PIVOT function to get results in the EXCEL row/column format.
SELECT [0],[1],[2]
FROM (
SELECT rownum
,colnum
,round(itemvalue, 4) as itemvalue
FROM wct.MINVERSE_q(
'SELECT 1,2,4 UNION ALL
SELECT 0,4,-6 UNION ALL
SELECT 14,7,1'
)) M PIVOT (
MAX(ItemValue)
FOR colnum IN ([0],[1],[2])
) AS pvt
This produces the following result.
To confirm that this is the inverse, we can use the MMULT_q function to see if the identity matrix is returned.
SELECT rownum
,colnum
,round(itemvalue,12)
FROM wct.MMULT_q(
'SELECT 1,2,4 UNION ALL
SELECT 0,4,-6 UNION ALL
SELECT 14,7,1'
,'SELECT [0],[1],[2]
FROM (
SELECT *
FROM wct.MINVERSE_q(' + wct.QUOTES(
'SELECT 1,2,4 UNION ALL
SELECT 0,4,-6 UNION ALL
SELECT 14,7,1') + '
)) M PIVOT (
MAX(ItemValue)
FOR colnum IN ([0],[1],[2])
) AS pvt'
)
This produces the following result.
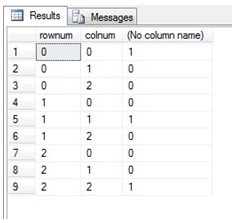
As we can see, the identity matrix, in 3rd normal form, is returned.
There are multiple versions of the matrix inverse functions, just as with the matrix product functions. Use the MINVERSE function for simple queries on tables or views for non-normalized data. Use the MINVERSEN function for simple queries on tables or views for non-normalized data. Use MINVERSE_q for more complex queries, including ‘on-the-fly’ calculations on non-normalized data. Use MINVERSEN_q for more complex queries, including ‘on-the-fly’ calculations on normalized data.
The matrix determinant function is a scalar-valued function, taking multiple rows (and columns) as input, but returning a single value. Like the matrix product and the matrix inverse functions, the matrix determinant functions in XLeratorDB come in multiple flavors. Use MDETERM for simple queries to calculate the matrix determinant on non-normalized data contained in a table or view. Use MDETERM_q for more complex queries, including ‘on-the-fly’ calculations, on non-normalized data. Use MDETERMN for simple queries to calculate the matrix determinant on data in 3rd normal for contained in a table or view. Use MDETERMN_q for more complex queries, including on-the-fly calculations, on data in 3rd normal form.
Here’s how the determinant function looks in EXCEL.
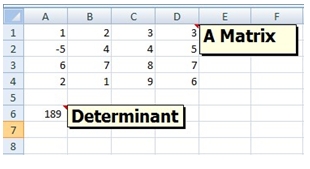
Here’s how we would calculate it in SQL Server using the MDETERM_q function.
SELECT wct.MDETERM_q(
'SELECT 1,2,3,3 UNION ALL
SELECT -5,4,4,5 UNION ALL
SELECT 6,7,8,7 UNION ALL
SELECT 2,1,9,6'
)
This produces the following result.
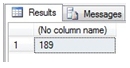
If the data were in a table in 3rd normal form, we could use the MDETERMN function. First, lets put the data into the #matrix table we defined above:
INSERT INTO #matrix
SELECT '1A',0,0,1 UNION ALL
SELECT '1A',0,1,2 UNION ALL
SELECT '1A',0,2,3 UNION ALL
SELECT '1A',0,3,3 UNION ALL
SELECT '1A',1,0,-5 UNION ALL
SELECT '1A',1,1,4 UNION ALL
SELECT '1A',1,2,4 UNION ALL
SELECT '1A',1,3,5 UNION ALL
SELECT '1A',2,0,6 UNION ALL
SELECT '1A',2,1,7 UNION ALL
SELECT '1A',2,2,8 UNION ALL
SELECT '1A',2,3,7 UNION ALL
SELECT '1A',3,0,2 UNION ALL
SELECT '1A',3,1,1 UNION ALL
SELECT '1A',3,2,9 UNION ALL
SELECT '1A',3,3,6
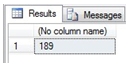
Then we can calculate the matrix determinant.
SELECT wct.MDETERMN(
'#matrix'
,'rowno'
,'colno'
,'val'
,'MatrixID'
,'1A'
)
This produces the following result.
We think that the matrix functions are a powerful addition to XLeratorDB/math library and have many uses in finance, engineering, and communications. We hope that you will find them useful, as well.
You can download the free 15-day Trial version of XLeratorDB/math here.