Cellular Automata in SQL Server
Feb
28
Written by:
Charles Flock
2/28/2020 4:44 PM

Based on Stephen Wolfram’s elementary cellular automata we demonstrate a very simple, straightforward approach to generating the cells for all 256 rules.
About 2 years ago I was watching a video of an MIT lecture on AGI (Artificial General Intelligence) given by Stephen Wolfram. He made several refences during the course of the lecture to his development of elementary cellular automata. During the course of the lecture, I thought it would be interesting to implement cellular automata in Excel without using VBA. Ultimately, that led to trying to do the same thing in SQL Server.
Here’s the output from Excel for rule 131 (there are 256 rules numbered from 0 to 255).
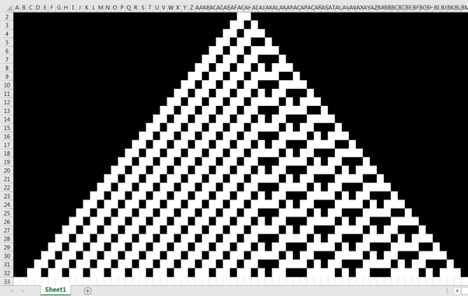
According to Wolfram Alpha, Rule 131 can be expressed with the following operation:
(p, q, r) ↦ (NOT (p XOR q)) AND (r OR (NOT p))
and not knowing any better, I used this logic and some conditional formatting to come up with the Excel solution. As these are elementary cellular automata, the logic is actually pretty simple. Each row in the Excel worksheet is based on the previous row. The p, q and r values are the Left, Center and Right cells from the previous row. The only value is the cells are 0 or 1. We end up with something that looks like this:

We can then apply some conditional formatting so that cells containing 1 are black and cells containing 0 are white. This results in the following representation of rule 131 in Excel.

Here’s a way of implementing that logic in SQL Server:
SELECT
x
,~(p^q)&(r|~p) as val
FROM (
SELECT
CAST(x as CHAR(3)) as x
,CAST(SUBSTRING(x,1,1) as bit) as p
,CAST(SUBSTRING(x,2,1) as bit) as q
,CAST(SUBSTRING(x,3,1) as bit)as r
FROM (
SELECT
wct.DEC2BIN(SeriesValue,3) as x
FROM
wct.SeriesInt(7,0,-1,NULL,NULL)
)n
)p
This produces the following result for Rule 131.
All that remains is to convert the bit values into either dark spaces or white spaces. In the following SQL I am using the Unicode Full Block character and space to do that.
SELECT
x
,~(p^q)&(r|~p) as val
,CAST(REPLACE(REPLACE(x,'1',NCHAR(9608)),'0',SPACE(1)) as NCHAR(3)) as x
,CAST(REPLACE(REPLACE(~(p^q)&(r|~p),'1',NCHAR(9608)),'0',SPACE(1)) as NCHAR(1)) as val
FROM (
SELECT
CAST(x as CHAR(3)) as x
,CAST(SUBSTRING(x,1,1) as bit) as p
,CAST(SUBSTRING(x,2,1) as bit) as q
,CAST(SUBSTRING(x,3,1) as bit)as r
FROM (
SELECT
wct.DEC2BIN(SeriesValue,3) as x
FROM
wct.SeriesInt(7,0,-1,NULL,NULL)
)n
)p
This produces the following result for Rule 131.
At this point, I paused in my thinking. Wolfram calls these ‘elementary cellular automata’. This seemed a little harder than elementary. It seemed like I would have to code a different combination of bit-wise operation for each rule; 256 rules. That seemed like a lot of work.
I tried coming at the problem from a different angle. I wondered why it was called Rule 131. The following SQL reveals the answer to that question.
SELECT
CAST(wct.BIN2DEC(STRING_AGG(val,
'') WITHIN GROUP (
ORDER BY x DESC)) as tinyint) as [Rule]
FROM
(
SELECT
x ,
~(p^q)&(r |~ p) as val
FROM
(
SELECT
CAST(x as CHAR(3)) as x ,
CAST(SUBSTRING(x, 1, 1) as bit) as p ,
CAST(SUBSTRING(x, 2, 1) as bit) as q ,
CAST(SUBSTRING(x, 3, 1) as bit)as r
FROM
(
SELECT
wct.DEC2BIN(SeriesValue,
3) as x
FROM
wct.SeriesInt(7,
0,
-1,
NULL,
NULL) )n )p )q
This produces the following result.
In binary, the value of 131 is expressed as 10000011, the exact pattern we see returned from our first SQL statement. All the rules work this way. And, if we treat the binary representation of the rule as a string, we can simply search the string to get the correct value. However, since 111 (decimal value 7) returns the left-most value and 000 (decimal value 0) returns the right-most value, the simplest thing to do is reverse the string. I used the following SQL to generate the return values for Rule 131.
SELECT
CAST(wct.DEC2BIN(k.seriesValue,
3) as char(3)) as binval ,
SUBSTRING(REVERSE(wct.DEC2BIN(131, 8)), k.SeriesValue + 1, 1) as binrule
FROM
wct.SeriesInt(7,
0,
-1,
NULL,
NULL)k
This returns the following result:
This approach works for every Rule. In the following SQL we generate all the possible outcomes for Rules 0 to 255 and pivot the results to make it easier to read.
DECLARE @ColumnName as nvarchar(max);
DECLARE @DynamicPivot as nvarchar(max);
CREATE TABLE #CA ( binval char(3) ,
numrule int ,
binrule char(1) ,
PRIMARY KEY (binval,
numrule) );
INSERT
INTO
#CA
SELECT
wct.DEC2BIN(k.seriesValue,
3) as binval ,
l.seriesvalue as numrule ,
SUBSTRING(REVERSE(wct.DEC2BIN(l.seriesvalue, 8)), k.SeriesValue + 1, 1) as binrule
FROM
wct.SeriesInt(0,
7,
NULL,
NULL,
NULL)k CROSS APPLY wct.SeriesInt(0,
255,
NULL,
NULL,
NULL)l;
--Create Dynamic PIVOT
SELECT
@ColumnName = ISNULL(@ColumnName + ',',
'') + QUOTENAME(SeriesValue)
FROM
wct.SeriesInt(0,
255,
NULL,
NULL,
NULL);
--Prepare the PIVOT query
SET
@DynamicPivot = N'SELECT binval, ' + @ColumnName + '
FROM
#CA
PIVOT(MAX(binrule) For numrule IN (' + @ColumnName + ')) as pvt
ORDER BY binval DESC';
--Execute the dynamic pivot
EXEC sp_executesql @DynamicPivot;
This produces the following result.
Now, we are ready to write some SQL. We will use a simple initial condition: all zeroes except for the center value which is set to 1. We can think of the length of that string as the size, and we can think of the number of evolutions as the steps. In this particular approach, each row will be a step which consists of 2*@steps columns. And, each row is generated based on the previous row.
We will create a temporary table (#ca) to store the left (L), center (C) and Right (R) values from the previous row as well as the value to be generated for the Rule. All values are converted to binary and stored in the table. We create a table (#grid) to store the ‘evolution’.
The #grid table is in 3rd-normal form and is keyed by row (r) and column (c). We use the LAG function to get the left value and the LEAD function to get the right value. There are some decisions to made about calculations at the boundaries (when column = 1 or column = s * @steps + 1); you can see this in the default values for the LEAD and LAG functions. Additionally, I have arbitrarily set column 1 to 1 in all cases, simply to maintain consistency with the Wolfram Alpha example and the Excel implementation.
I use the Results to Text option in SSMS and then shrink the size of the output.
DECLARE @rule as int = 131;
SET
NOCOUNT ON;
--Table to store the (L)eft, (C)enter, (R)ight and Rule values
CREATE TABLE #ca ( L int ,
C int ,
R int ,
binrule CHAR(1) ,
Primary Key(L,
C,
R) );
--Generate the values for this rule
INSERT
INTO
#ca
SELECT
SUBSTRING(wct.DEC2BIN(k.seriesValue, 3), 1, 1) as L ,
SUBSTRING(wct.DEC2BIN(k.seriesValue, 3), 2, 1) as C ,
SUBSTRING(wct.DEC2BIN(k.seriesValue, 3), 3, 1) as R ,
SUBSTRING(REVERSE(wct.DEC2BIN(@rule, 8)), k.SeriesValue + 1, 1) as binrule
FROM
wct.SeriesInt(0,
7,
NULL,
NULL,
NULL)k;
--table to store the evolution
CREATE TABLE #grid ( r int ,
c int ,
x int ,
PRIMARY KEY(r,
c) );
--Initialize the values for the evolution
DECLARE @i as int = 0;
DECLARE @steps as int = 32;
--simple initial condition
INSERT
INTO
#grid
SELECT
0 as r ,
seq as c ,
CASE
k.SeriesValue
WHEN @steps THEN 1
ELSE 0
END as x
FROM
wct.SeriesInt(1,
2 * @steps + 1,
NULL,
NULL,
NULL)k;
--Evolve
WHILE @i < @steps-1
BEGIN
--increment the counter
SET
@i = @i + 1
--calculate the boolean value
INSERT
INTO
#grid
SELECT
@i as r ,
n.c ,
CASE
n.c
WHEN 1 THEN 1
ELSE #ca.binrule
END
FROM
(
SELECT
g.c ,
LAG(g.x,
1,
1) OVER (
ORDER BY g.c ASC) as P ,
g.x as Q ,
LEAD(g.x,
1,
1) OVER (
ORDER BY g.c ASC) AS R
FROM
#grid g
WHERE
g.r = @i-1 )n
INNER JOIN #ca ON
n.P = #ca.L
AND n.Q = #ca.C
AND n.R = #ca.R
END;
--Format the output
SELECT
REPLACE(REPLACE(STRING_AGG(x, '') WITHIN GROUP (ORDER BY c ASC), '1', NCHAR(9608)), '0', SPACE(1))
FROM
#grid
GROUP BY
r
ORDER BY
r ASC
This produces the following result:

which is a pretty good facsimile of the Excel representation at the beginning of this article. If we wanted to see what it looks like after 100 evolutions, we simply change the @steps variable to 100.

Cellular automata become really interesting, though, when the initial conditions are random; meaning a random sequence of zeroes and ones. If we make the following change to our SQL:
--simple initial condition
INSERT
INTO
#grid
SELECT
0 as r ,
seq as c,
--CASE k.SeriesValue
-- WHEN @steps THEN 1
-- ELSE 0
--END as x
wct.RANDBETWEEN(0,
1) as x
FROM
wct.SeriesInt(1,
2 * @steps + 1,
NULL,
NULL,
NULL)k;
we get the following result.
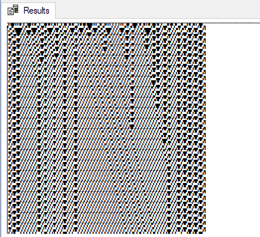
While I think that this a pretty good representation of how the very simple rules behind elementary cellular automata can lead to quite complex designs, I am not quite happy with this implementation. This approach requires looping which I always want to avoid in SQL as I like everything to be set-based. Because of this, scaling up is definitely an issue. Since we are looping through and inserting rows into our table, the table size is expanding geometrically. That’s a lot of overhead. If we had a size of 1,000 and we wanted to do 1,000 steps, we would end up with 1,000,000 rows in the #grid table.
The obvious solution is to use a recursive Common Table Expression (CTE). But the CTE implementation is tricky. The recursive CTE is obvious because each row is exclusively based on the previous row which is exactly what the recursive CTE is designed for. But each step is an aggregate of the application of the Rule to each position in the previous step; and the CTE does not permit aggregates. Further, while each recursion can calculate multiple columns, it can only embody 1 row.
Given these limitations, the only way to use the CTE was to make each row a string of ones and zeroes. The CTE anchor would be our initial condition and then each iteration would apply rule.
I decided to create a used-defined function (UDF) to do this. This turned out to be very interesting, because while aggregate functions cannot be used in the CTE, using the STRING_AGG function in the UDF worked just fine. This what the function looks like.
DROP FUNCTION IF EXISTS dbo.CA
GO
CREATE FUNCTION dbo.CA (
@step as varchar(max) ,
@rule tinyint )
RETURNS
varchar(max) AS
BEGIN
DECLARE @result varchar(max)
DECLARE @binrule as CHAR(8) = REVERSE(wct.DEC2BIN(@rule,
8))
DECLARE @len as int = LEN(@step) SET
@result = (
SELECT
STRING_AGG(SUBSTRING(@binrule, cast(wct.BIN2DEC(x) as int)+ 1, 1),
'') WITHIN GROUP (
ORDER BY c ASC)
FROM
(
SELECT
k.seriesvalue as c ,
CASE
k.Seriesvalue
WHEN 1 THEN CONCAT('0', SUBSTRING(@step, 1, 2))
WHEN @len THEN CONCAT(SUBSTRING(@step, @len-1, 2), '0')
ELSE SUBSTRING(@step, k.seriesvalue-1, 3)
END as x
FROM
wct.SeriesInt(1,
@len,
NULL,
NULL,
NULL)k )n ) RETURN @result
END
All that needs to be passed into the function is the step and the rule. Note that I have made one change from our previous example with respect to boundary conditions. At position 1 of the step, there is no left (L) value. If we only decoded using the center and right values the only possible values would be 00, 01, 10 and 11. By adding a preceding 0 we maintain consistency with those values, whereas in our previous examples we were actually changing the values to 100, 101, 110 or 111. We applied similar logic to the nth position (where n = length of the string) so that we append a zero as the rightmost value.
We now use this function in our recursive CTE.
DECLARE @step as varchar(max);
DECLARE @rule as int = 110;
DECLARE @size as int = 1000;
DECLARE @steps as int = 150;
--Stable Starting Point
--SET @step = STUFF(REPLICATE('0',@size),@size / 2,1,'1');
--Random Starting point
SET
@STEP = (
SELECT
STRING_AGG(SeriesValue,
'') WITHIN GROUP (
ORDER BY seq ASC)
FROM
wct.Seriesint(0,
1,
NULL,
@size,
'R'));
with mycte as (
SELECT
1 as rn ,
@step as step
UNION ALL
SELECT
rn + cast(1 as int) ,
dbo.CA(step,
@rule)
FROM
mycte
WHERE
rn < @steps )
SELECT
REPLACE(REPLACE(STEP, '1', NCHAR(9608)), '0', SPACE(1))
FROM
mycte
ORDER BY
rn OPTION (MAXRECURSION 0)
This produces the following result.

Note that I have set the rule to Rule 110 while our previous example was rule 131. Rule 110 is generally considered to be Turing-complete and I simply wanted demonstrate how to do this in SQL (making SQL Turing complete, QED).
I have also included, but commented out, SQL for a stable starting condition. You can uncomment that, and comment out the SQL for a random starting point.
Here are some other rules all generated with this SQL.

You can find out more about cellular automata by going to Wolfram Alpha and in Wikipedia. This example gave me the opportunity to really dive into the logic behind cellular automata, which is really quite fascinating. It’s very interesting how the application of a very simple can produce unpredictable results (paraphrasing Wolfram himself). It’s also quite interesting to see what you can do in SQL with just a couple of the XLeratorDB functions. You should download the 15-day trial and tell us what you think.