Generalized Birthday Problem
Jun
14
Written by:
Charles Flock
6/14/2017 4:47 PM

In November 2008, we wrote about the birthday paradox. In this article, we talk about techniques to solve birthday problems where we want to calculate the likelihood of 3, 4, 5, or more people in a room having the same birthday. We particularly focus on the techniques in E.H. McKinney’s 1966 paper and show easily SQL lends itself to exact solutions for these types of problems.
Sooner or later in most high school statistics courses students are presented with following problem; “How many people need to be in a room for there to be a 50% chance of 2 people having the same birthday?” This problem, known as the birthday paradox (which we wrote about in 2011), serves as an introduction into basic combinatorics and is appealing because the solution is surprising.
Here’s a very easy way to calculate the answer in SQL, using the XLeratorDB PERMUT function.
DECLARE @x as int = 2
DECLARE @p as float = 1-wct.PERMUT(365,@x)*wct.POWER(365,-@x)
WHILE @p < 0.5
BEGIN
SET @x = @x + 1
SET @p = 1-wct.PERMUT(365,@x)*wct.POWER(365,-@x)
END
SELECT @x as N
This produces the following result.
In this article, we are going to explore techniques for calculating the number of people required to be in a room for there to be a 50% chance for 3, 4, 5, 6 or more people to have the same birthday. The math behind this is based on E. H. McKinney’s Generalized Birthday Problem which appeared in The American Mathematical Monthly Vol. 73, No. 4 (Apr. 1966) pp. 385 – 387.
3 people having the same birthday
Using McKinney’s formulation, the probability of three people having the same birthday in a room of size n can be defined as:
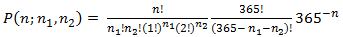
The term P(n;n1,n2 ) is the probability that no birthday is shared k or more times in a specific arrangement of n people. The real challenge, then, is coming up with all the possible arrangements of n people, something that is actually quite simple to do in SQL. Let’s look at an example.
In a room with 10 people, we are looking for all the combinations of n1 + n2 = 10, where n1 is the number of non-repeated items and n2 is the number or pairs. With such a small number, it’s easy to see all the possible arrangements.
We can use the XLeratorDB SeriesInt function to generate these combinations in SQL. Here’s one way to do that.
DECLARE @people as float = 10
DECLARE @k as float = 3
SELECT
@people-2*x2.SeriesValue as n1
,x2.SeriesValue as n2
FROM
wct.Seriesint(0,Floor(@people/(@k-1)),NULL,Null,NULL)x2
This produces the following result.
The calculation of P(n;n1,n2 ) is performed for each arrangement, as can be seen in this SQL.
This produces the following result.
Obviously, then, the probability is defined as:
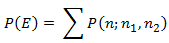
where E is defined as the event that, for each birthday, the number of people with that birthday is at most k – 1. This gets us to McKinney’s final formula for calculating the probability of interest:
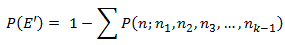
It’s then a simple matter to add McKinney’s calculation to our SQL for this example. This requires using the XLeratorDB FACT and PERMUT functions.
This produces the following result.
This means that in a room with 10 people, the probability that 3 people have the same birthday is approximately 0.0888%.
All that remains to be done is to iterate through the number people until we get to the first solution where the probability is greater than 50%. We know that this number has to be greater than 23 since that was the solution for 2 people having the same birthday. Here’s SQL that comes up with the solution.
This produces the following result.
In a room with 88 people there is a 51.1065% probability that 3 people have the same birthday and there are 45 possible arrangements. With 87 people in the room the probability is 49.9455% and the number of arrangements is 44.
If we wanted to see each arrangement of the 88 people and its probability we could run the following SQL.
This produces the following result.
4 people having the same birthday
Let’s look at how to change our SQL to calculate the number people required to have a 50% probability of 4 having the same birthday. The formula for this is:
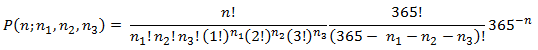
Obviously, this is very similar to the formula used for 3 people having the same birthday except that we will be evaluating arrangements consisting of 3 columns rather than 2 columns. However, before writing that SQL we need to address the use of the factorial function in these calculations. In 64-bit floating point math, the maximum value that can be entered in the factorial function is 170; anything greater than that creates arithmetic overflow.
We need to change our SQL to use natural logarithms. This is a relatively straightforward process where we will substitute the XLeratorDB FACTLN function for the FACT function and the XLeratorDB LPERMUT function for the PERMUT function. We then use the EXP function to convert the log of the probability to the probability. This also gives us the opportunity to improve performance a little bit by eliminating redundant calculations. We can add some variables and change the SQL to return the probability across all combinations.
DECLARE @nday as float = 365
DECLARE @people as float = 88
DECLARE @k as float = 4
DECLARE @p as float = 0
DECLARE @m as float = 0
DECLARE @lfact1 as float = wct.FACTLN(1)
DECLARE @lfact2 as float = wct.FACTLN(2)
DECLARE @lfact3 as float = wct.FACTLN(3)
DECLARE @lfactpeople as float
DECLARE @ldenom as float
WHILE @p < 0.5
BEGIN
SET @people = @people + 1
SET @lfactpeople = wct.FACTLN(@people)
SET @ldenom = @people*LOG(@nday)
SELECT
@p = 1 - SUM(EXP(@lfactpeople-(wct.FACTLN(n1)+wct.FACTLN(n2)+wct.FACTLN(n3)+n1*@lfact1+n2*@lfact2+n3*@lfact3)+wct.LPERMUT(@nday,n1+n2+n3)-@ldenom))
,@m = COUNT(*)
FROM (
SELECT
@people-(3*x3.SeriesValue + 2*x2.SeriesValue) as n1
,x2.SeriesValue as n2
,x3.SeriesValue as n3
FROM
wct.Seriesint(0,Floor(@people/(@k-1)),NULL,Null,NULL)x3
CROSS APPLY
wct.Seriesint(0,Floor((@people -3*x3.SeriesValue)/(@k-2)),NULL,Null,NULL)x2
)n
END
SELECT
@people as [people], @p as [probability], @m as arrangements
This produces the following result.
In going from three birthdays to four birthdays the number of people went from 88 to 187 and the number of arrangements went from 45 to 3008. The processing time went from under a second to about 3 seconds. Of course, in this SQL we calculated the probability for every value from 89 to 187, which is fine for small amounts of data, but we will look at better ways get the result when we look at 5 people having the same birthday.
5 people having the same birthday
We change our formula from the previous example to:
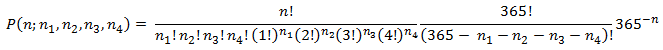
We can modify our SQL from the previous example for k = 5.
DECLARE @nday as float = 365
DECLARE @people as float = 187
DECLARE @k as float = 5
DECLARE @p as float = 0
DECLARE @m as float = 0
DECLARE @lfact1 as float = wct.FACTLN(1)
DECLARE @lfact2 as float = wct.FACTLN(2)
DECLARE @lfact3 as float = wct.FACTLN(3)
DECLARE @lfact4 as float = wct.FACTLN(4)
DECLARE @lfactnday as float = wct.FACTLN(@nday)
DECLARE @lfactpeople as float
DECLARE @ldenom as float
WHILE @p < 0.5
BEGIN
SET @people = @people + 1
SET @lfactpeople = wct.FACTLN(@people)
SET @ldenom = @people*LOG(@nday)
SELECT
@p = 1 - SUM(EXP(@lfactpeople-(wct.FACTLN(n1)+wct.FACTLN(n2)+wct.FACTLN(n3)+wct.FACTLN(n4)+n1*@lfact1+n2*@lfact2+n3*@lfact3+n4*@lfact4)+wct.LPERMUT(@nday,n1+n2+n3)-@ldenom))
,@m = COUNT(*)
FROM (
SELECT
@people-(4*x4.SeriesValue + 3*x3.SeriesValue + 2*x2.SeriesValue) as n1
,x2.SeriesValue as n2
,x3.SeriesValue as n3
,x4.SeriesValue as n4
FROM
wct.Seriesint(0,Floor(@people/(@k-1)),NULL,Null,NULL)x4
CROSS APPLY
wct.Seriesint(0,Floor((@people - 4*x4.SeriesValue)/(@k-2)),NULL,Null,NULL)x3
CROSS APPLY
wct.Seriesint(0,Floor((@people - 4*x4.SeriesValue - 3*x3.SeriesValue)/(@k-3)),NULL,Null,NULL)x2
)n
END
SELECT
@people as [people], @p as [probability], @m as arrangements
This produces the following result.
In going from four birthdays to five birthdays the number of people went from 187 to 313 and the number of arrangements went from 3,008 to 223,829. The processing time went from about 3 seconds to just under 5 minutes. As in the previous example, we calculated the probability for every value from 187 to 313.
Up to this point we have found solutions simply be monotonically increasing the number of people calculating the probability. In this SQL we have modified that approach to us the secant method to find a solution.
DECLARE @nday as float = 365
DECLARE @people as float
DECLARE @k as float = 5
DECLARE @mxn as float = 0
DECLARE @mxnminus1 as float = 0
DECLARE @lfact1 as float = wct.FACTLN(1)
DECLARE @lfact2 as float = wct.FACTLN(2)
DECLARE @lfact3 as float = wct.FACTLN(3)
DECLARE @lfact4 as float = wct.FACTLN(4)
DECLARE @lfactnday as float = wct.FACTLN(@nday)
DECLARE @lfactpeople as float
DECLARE @ldenom as float
DECLARE @start as float = 187
DECLARE @xn as float =NULL
DECLARE @xnminus1 as float = NULL
DECLARE @xnminus2 as float = NULL
DECLARE @fxn as float
DECLARE @fxnminus1 as float
DECLARE @fxnminus2 as float
DECLARE @solved as bit = 0
WHILE @solved = 0
BEGIN
SET @xnminus2 = @xnminus1
SET @xnminus1 = @xn
SET @fxnminus2 = @fxnminus1
SET @fxnminus1 = @fxn
SET @mxnminus1 = @mxn
SET @xn = IIF(@xn IS NULL,@start,IIF(@xnminus2 IS NULL,@xn+100,CEILING(@xnminus1-@fxnminus1*(@xnminus1-@xnminus2)/(@fxnminus1-@fxnminus2))))
IF @xn = @xnminus1
IF @fxn > 0
BEGIN
SET @xn = IIF(@fxn > 0,@xn-1,@xn+1)
END
SET @people = @xn
SET @lfactpeople = wct.FACTLN(@people)
SET @ldenom = @people*LOG(@nday)
SELECT
@fxn = 0.5 - (SUM(ISNULL(EXP(@lfactpeople-(wct.FACTLN(n1)+wct.FACTLN(n2)+wct.FACTLN(n3)+wct.FACTLN(n4)+n1*@lfact1+n2*@lfact2+n3*@lfact3+n4*@lfact4)+wct.LPERMUT(@nday,n1+n2+n3+n4)-@ldenom),0)))
,@mxn = COUNT(*)
FROM (
SELECT
@people-(4*x4.SeriesValue + 3*x3.SeriesValue + 2*x2.SeriesValue) as n1
,x2.SeriesValue as n2
,x3.SeriesValue as n3
,x4.SeriesValue as n4
FROM
wct.Seriesint(0FLOOR(@people/(@k-1)),NULL,Null,NULL)x4
CROSS APPLY
wct.Seriesint(0,FLOOR((@people - 4*x4.SeriesValue)/(@k-2)),NULL,Null,NULL)x3
CROSS APPLY
wct.Seriesint(0,FLOOR((@people - 4*x4.SeriesValue - 3*x3.SeriesValue)/(@k-3)),NULL,Null,NULL)x2
)n
IF @xnminus1 IS NOT NULL
BEGIN
IF ABS(@xn - @xnminus1) <= 1
BEGIN
SET @solved = 1
IF @fxn > 0
SELECT @xn as [People], @fxn + 0.5 as [probability], @mxn as [arrangements]
ELSE
SELECT @xnminus1 as [People], @fxnminus1 + 0.5 as [probability], @mxnminus1 as [arrangements]
END
END
END
This produces the following result.
This ran in just under 10 seconds, a significant improvement. Notice that we wrapped our calculation in an ISNULL to capture situations where we might be trying to calculate the factorial of a negative number (which is undefined) and, without going into the math, in those situations the probability for that arrangement is zero. We also changed the calculation to of the probability to be the probability minus 0.5, since we are looking for the closest integer value that renders f(x) = 0. This is always a little tricky for discrete functions like this.
We also need to use this approach as we do the calculation for 6 people having the same birthday as we can anticipate that we need to have more than 365 people in the room and the possible ways of arranging the birthdays will probably number in the millions.
6 people having the same birthday
We change our formula from the previous example to:
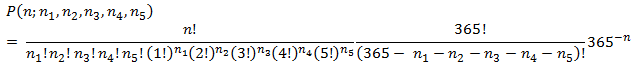
We then use the following SQL, which uses the secant method, to find the solution.
DECLARE @nday as float = 365
DECLARE @people as float
DECLARE @k as float = 6
DECLARE @mxn as float = 0
DECLARE @mxnminus1 as float = 0
DECLARE @lfact1 as float = wct.FACTLN(1)
DECLARE @lfact2 as float = wct.FACTLN(2)
DECLARE @lfact3 as float = wct.FACTLN(3)
DECLARE @lfact4 as float = wct.FACTLN(4)
DECLARE @lfact5 as float = wct.FACTLN(5)
DECLARE @lfactnday as float = wct.FACTLN(@nday)
DECLARE @lfactpeople as float
DECLARE @ldenom as float
DECLARE @start as float = 313
DECLARE @xn as float =NULL
DECLARE @xnminus1 as float = NULL
DECLARE @xnminus2 as float = NULL
DECLARE @fxn as float
DECLARE @fxnminus1 as float
DECLARE @fxnminus2 as float
DECLARE @solved as bit = 0
WHILE @solved = 0
BEGIN
SET @xnminus2 = @xnminus1
SET @xnminus1 = @xn
SET @fxnminus2 = @fxnminus1
SET @fxnminus1 = @fxn
SET @mxnminus1 = @mxn
SET @xn = IIF(@xn IS NULL,@start,IIF(@xnminus2 IS NULL,@xn+100,CEILING(@xnminus1-@fxnminus1*(@xnminus1-@xnminus2)/(@fxnminus1-@fxnminus2))))
IF @xn = @xnminus1
IF @fxn > 0
BEGIN
SET @xn = IIF(@fxn > 0,@xn-1,@xn+1)
END
SET @people = @xn
SET @lfactpeople = wct.FACTLN(@people)
SET @ldenom = @people*LOG(@nday)
SELECT
@fxn = 0.5 - (SUM(ISNULL(EXP(@lfactpeople-(wct.FACTLN(n1)+wct.FACTLN(n2)+wct.FACTLN(n3)+wct.FACTLN(n4)+wct.FACTLN(n5)+n1*@lfact1+n2*@lfact2+n3*@lfact3+n4*@lfact4+n5*@lfact5)+wct.LPERMUT(@nday,n1+n2+n3+n4+n5)-@ldenom),0)))
,@mxn = COUNT(*)
FROM (
SELECT
@people-(5*x5.SeriesValue + 4*x4.SeriesValue + 3*x3.SeriesValue + 2*x2.SeriesValue) as n1
,x2.SeriesValue as n2
,x3.SeriesValue as n3
,x4.SeriesValue as n4
,x5.SeriesValue as n5
FROM
wct.Seriesint(0,Floor(@people/(@k-1)),NULL,Null,NULL)x5
CROSS APPLY
wct.Seriesint(0,Floor((@people - 5*x5.SeriesValue)/(@k-2)),NULL,Null,NULL)x4
CROSS APPLY
wct.Seriesint(0,Floor((@people - 5*x5.SeriesValue - 4*x4.SeriesValue)/(@k-3)),NULL,Null,NULL)x3
CROSS APPLY
wct.Seriesint(0,Floor((@people - 5*x5.SeriesValue - 4*x4.SeriesValue - 3*x3.SeriesValue)/(@k-4)),NULL,Null,NULL)x2
)n
IF @xnminus1 IS NOT NULL
BEGIN
IF ABS(@xn - @xnminus1) <= 1
BEGIN
SET @solved = 1
IF @fxn > 0
SELECT @xn as [People], @fxn + 0.5 as [probability], @mxn as [arrangements]
ELSE
SELECT @xnminus1 as [People], @fxnminus1 + 0.5 as [probability], @mxnminus1 as [arrangements]
END
END
END
This produces the following result.
In going from five birthdays to six birthdays the number of people went from 313 to 460 and the number of arrangements went from 223,829 to 16,583,627. The processing time went from about 10 seconds to just over 16 minutes.
Clearly, 16 minutes for an exact solution is an awful lot of time. Let’s look at some techniques for estimating a solution.
Binomial approximation
The formula for the binomial approximation is:
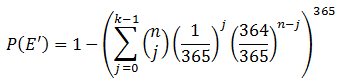
We can see how close this gets us to the exact result that we calculated for 6 people having the same birthday, with the following SQL.
This produces the following result.
Which is pretty close to the exact probability of 0.502449410370535. We could of course come up with a root-finding algorithm to zero in on the solution, but there is so little overhead that we can simply iterate from the starting point.
The following SQL calculates the number of people required for a 50% probability of k people having the same birthday for values of k from 6 to 15.
This produces the following result.
Poisson approximation
The formula for the Poisson approximation is:
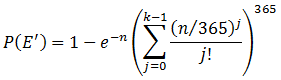
As we did with the binomial approximation, we can see how close this gets us to the exact result that we calculated for 6 people having the same birthday, with the following SQL.
This produces the following result.
And, the following SQL calculates the number of people required for a 50% probability of k people having the same birthday for values of k from 6 to 15 using the Poisson approximation.
This produces the following result.
Chi-square inverse approximation
This approach actually gives the appearance of being a closed-form solution (which certainly makes the SQL simpler) by taking advantage of the XLeratorDB CHISQ_INV function. However, there is no closed-form solution for calculating the inverse of the chi-square distribution; the root-finding algorithm is embedded in the function rather than having to be explicitly included in the SQL.
This SQL calculates the number of people required for a 50% probability of k people having the same birthday for values of k from 6 to 15 using the Chi-square inverse approximation.
DECLARE @p as float = 0.5
DECLARE @mu as float = -LOG(1 - @p)
DECLARE @N as float = 365
DECLARE @pi as float = @mu/@N
SELECT
SeriesValue as k,
0.5*wct.CHISQ_INV(@pi,2*SeriesValue)*@N as people
FROM
wct.SeriesInt(6,15,NULL,NULL,NULL)
This produces the following result.
It’s worth pointing out that there is a slightly simpler solution, which produces exactly the same results, using the XLeratorDB INVGAMMAP function.
DECLARE @p as float = 0.5
DECLARE @mu as float = -LOG(1 - @p)
DECLARE @N as float = 365
DECLARE @pi as float = @mu/@N
SELECT
SeriesValue as k,
wct.INVGAMMAP(@pi,seriesValue)*@N as people
FROM
wct.SeriesInt(6,15,NULL,NULL,NULL)
This produces the following result.
Conclusion
We were able to use McKinney’s techniques for the generalized birthday problem for 3, 4, 5, and 6 birthdays (which is actually more than McKinney) producing the exact number of people required, the exact probability and the number of different ways that people could be arranged. We also looked at approximation methods for 6 birthdays and beyond. And we did all this using a handful of XLeratorDB functions and SQL.
If you are interested in exploring the tremendous possibilities of doing statistical analysis using SQL, then download the 15-day trial of XLeratorDB. It includes over 900 functions, built specifically for SQL Server, including all the ones used in this article. If you discover that you need a function that’s not included, just let us know at support@westclintech.com.