New SQL Server loan functions in XLeratorDB/financial 1.13
Sep
25
Written by:
Charles Flock
9/25/2014 5:34 PM

We added 7 new table-valued functions to XLeratorDB/financial and XLeratorDB/financial 2008 that generate principal and interest payment schedules for different types of loans. This article provides insight into some of the calculations used in these new functions.
On September 19, 2014 we added 7 new table-valued functions to the XLeratorDB financial library that generate cash flow projections for a wide variety of loan types. Using these functions is as easy as using SQL and doesn't require any advanced knowledge of financial calculations. The functions insulate the user from the complexity of the calculations for these type of loans. The purpose of this article is to explore some of those complexities in more detail, especially the calculations of the principal payment, interest payment and grace interest amounts. We will do that by using SQL and other XLeratorDB functions. Knowing the how of the calculations, of course, is not necessary to use the functions and all of the examples provided in this article are really the hard way of doing things. Nothing could be easier than just using the new functions.
There are any number of ways to group the functions together. Let's start by splitting the functions into loans with fixed maturity dates and loans with no fixed maturity date.
Loans with no Fixed Maturity Dates
· Bullet - Single payment at maturity
· Balloon – periodic interest-only payments with the entire principal balance paid at maturity.
· ConstantPrincipal – the principal amount is amortized on a straight-line basis over the life of the loan.
Loans with no Fixed Maturity Date
· ConstantPaymentAmount – a fixed periodic payment is made until the loan is paid off. Unlike ConstantCashFlow where the periodic payment amount is calculated by the function, the periodic payment amount is an input to the function.
· ConstantPrincipalRate – a fixed percentage of principal is paid off periodically until the loan is paid off.
Date Calculations
One of the key aspects of understanding the loan calculations is understanding how the dates are calculated. We created the table-valued function PaymentPeriods function precisely for that reason. PaymentPeriods exposes the results of the date calculations used in the loan functions. You should clink on the link to the documentation to read more about it, but I will summarize the important points here:
· All dates are moved to the end of the month and all calculations use these end-of-month dates.
· The first payment date is calculated by the functions.
· All subsequent payments are calculated from the first payment date.
· If a calculated payment date lands in the grace period, then the payment date is moved to the end of the grace period and all remaining payment dates are calculated from the end of the grace period.
· Payment frequencies are always specified as the number of months between payments. For example, monthly payments would have a payment frequency of 1; quarterly payments would have a payment frequency of 3, semi-annual payments would have a payment frequency of 6, annual payments would have a payment frequency of 12.
Interest Calculations
In these new functions the interest portion of each cash flow is calculated using the following equation:
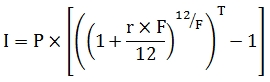
Where:
|
I
|
=
|
Interest Payment
|
|
P
|
=
|
Principal Amount
|
|
r
|
=
|
Interest Rate
|
|
F
|
=
|
Frequency
|
|
T
|
=
|
Time, in years, from the previous interest payment date to the current interest payment date
|
For example, let's say we had a 100,000 loan at an interest rate of 6.0% that pays interest semi-annually starting on 2014-06-30. The day-count convention is Actual/360. In SQL terms here's what the interest calculation would look like.
DECLARE @P as money = 100000
DECLARE @date_start as date = '2014-06-30'
DECLARE @date_end as date = '2014-12-31'
DECLARE @R as float = 0.06
DECLARE @basis as int = 2 --Actual/360
DECLARE @F as int = 6
SELECT
@P*(POWER(POWER((1+@R*@F/12),12/@F),wct.YEARFRAC(@date_start,@date_end,@basis))-1) as I
This produces the following result.
I
----------------------
3067.6790394899
This is all pretty conventional and straightforward stuff for the simpler loan types, which I would define as Bullet, Balloon, ConstantCashFlow, and ConstantPaymentAmount. The thing that these loans have in common is that there is a single repayment structure. In other words, I don't have to account for the principal balance changing between interest payment dates. We could replicate the interest (and principal) calculations for a loan with a periodic interest payment and a single payment of interest at maturity with the following SQL.
DECLARE @P as money = 100000
DECLARE @date_start as date = '2014-06-30'
DECLARE @date_end as date = '2019-12-31'
DECLARE @R as float = 0.06
DECLARE @basis as int = 2 --Actual/360
DECLARE @F as int = 6
;WITH mycte as (
SELECT
0 as Period,
@date_start as PaymentDate,
@P as Principal,
0e+00 as InterestPayment,
CAST(0 as money) as PrincipalPayment
UNION ALL
SELECT
Period + 1,
CAST(wct.EOMONTH(PaymentDate, @F) as date),
CASE
WHEN CAST(wct.EOMONTH(PaymentDate, @F) as date) = @date_end THEN 0
ELSE Principal
END,
Principal *(POWER(POWER(1+@R*@F/12e+00, 12e+00/@F), wct.YEARFRAC(LAG(PaymentDate,1,PaymentDate) OVER (ORDER BY PERIOD),CAST(wct.EOMONTH(PaymentDate, @F) as date),@basis)) - 1),
CASE
WHEN CAST(wct.EOMONTH(PaymentDate, @F) as date) = @date_end THEN Principal
ELSE 0
END
FROM
mycte
WHERE
PaymentDate < @date_end
)
SELECT
*
FROM
mycte
Or, you could just enter this SQL:
SELECT
Period,
PaymentDate,
CapitalAmountInDebt as Principal,
InterestPayment,
PrincipalPayment,
CashFlow
FROM wct.Balloon(
100000 --@OutstandingAmount
,'Actual/360' --@InterestBasis
,.06 --@InterestRate
,6 --@PaymentFrequency
,'2019-12-31' --@MaturityDate
,'2014-06-30' --@ReferenceDate
,NULL --@PrevPayDate
,NULL --@StartDate
,NULL --@FirstPayDate
,NULL --@GracePeriodStartDate
,NULL --@GracePeriodEndDate
)
Either way, you get the following result.
|
Period
|
PaymentDate
|
Principal
|
InterestPayment
|
PrincipalPayment
|
CashFlow
|
|
0
|
2014-06-30
|
100000
|
0.0000
|
0
|
0.0000
|
|
1
|
2014-12-31
|
100000
|
3067.6790
|
0
|
3067.6790
|
|
2
|
2015-06-30
|
100000
|
3016.9156
|
0
|
3016.9156
|
|
3
|
2015-12-31
|
100000
|
3067.6790
|
0
|
3067.6790
|
|
4
|
2016-06-30
|
100000
|
3033.8340
|
0
|
3033.8340
|
|
5
|
2016-12-31
|
100000
|
3067.6790
|
0
|
3067.6790
|
|
6
|
2017-06-30
|
100000
|
3016.9156
|
0
|
3016.9156
|
|
7
|
2017-12-31
|
100000
|
3067.6790
|
0
|
3067.6790
|
|
8
|
2018-06-30
|
100000
|
3016.9156
|
0
|
3016.9156
|
|
9
|
2018-12-31
|
100000
|
3067.6790
|
0
|
3067.6790
|
|
10
|
2019-06-30
|
100000
|
3016.9156
|
0
|
3016.9156
|
|
11
|
2019-12-31
|
0
|
3067.6790
|
100000
|
103067.6790
|
However for ConstantPrincipal, ConstantPrincipalAmount and ConstantPrincipalRate this formula needs to be adjusted for the cases where the principal balance changes between interest payment dates. Let's look at how that calculation works using the example above.
The first thing that we are going to do is to break up the calculation into monthly pieces. This SQL gets us started by generating a date and a principal amount for each month in the interest period.
DECLARE @P as money = 100000
DECLARE @date_start as date = '2014-06-30'
DECLARE @date_end as date = '2014-12-31'
DECLARE @R as float = 0.06
DECLARE @basis as int = 2 --Actual/360
DECLARE @F as int = 6
;WITH mycte as (
SELECT
0 as Period,
@date_start as PaymentDate,
@P as Principal
UNION ALL
SELECT
Period + 1,
CAST(wct.EOMONTH(PaymentDate, 1) as date),
Principal
FROM
mycte
WHERE
PaymentDate < @date_end
)
SELECT
*
FROM
mycte
This produces the following result.
|
Period
|
PaymentDate
|
Principal
|
|
0
|
2014-06-30
|
100000
|
|
1
|
2014-07-31
|
100000
|
|
2
|
2014-08-31
|
100000
|
|
3
|
2014-09-30
|
100000
|
|
4
|
2014-10-31
|
100000
|
|
5
|
2014-11-30
|
100000
|
|
6
|
2014-12-31
|
100000
|
Now, we can modify the SQL in the CTE to calculate the interest for each period using our interest formula from above.
;WITH mycte as (
SELECT
0 as Period,
@date_start as PaymentDate,
@P as Principal
UNION ALL
SELECT
Period + 1,
CAST(wct.EOMONTH(PaymentDate, 1) as date),
Principal
FROM
mycte
WHERE
PaymentDate < @date_end
)
SELECT
*,
LAG(Principal,1,0) OVER (ORDER BY PERIOD) *(POWER(POWER(1+@R * @F/12e+00, 12e+00/@F), wct.YEARFRAC(LAG(PaymentDate,1,NULL) OVER (ORDER BY PERIOD),PaymentDate,2)) - 1) As AI
FROM
mycte
This produces the following result.
|
Period
|
PaymentDate
|
Principal
|
AI
|
|
0
|
2014-06-30
|
100000
|
0
|
|
1
|
2014-07-31
|
100000
|
510.3662
|
|
2
|
2014-08-31
|
100000
|
510.3662
|
|
3
|
2014-09-30
|
100000
|
493.8622
|
|
4
|
2014-10-31
|
100000
|
510.3662
|
|
5
|
2014-11-30
|
100000
|
493.8622
|
|
6
|
2014-12-31
|
100000
|
510.3662
|
However, if we add up all the AI values, it will not equal the interest value that we originally calculated.
;WITH mycte as (
SELECT
0 as Period,
@date_start as PaymentDate,
@P as Principal
UNION ALL
SELECT
Period + 1,
CAST(wct.EOMONTH(PaymentDate, 1) as date),
Principal
FROM
mycte
WHERE
PaymentDate < @date_end
)
SELECT
SUM(AI) as I
FROM (
SELECT
*,
LAG(Principal,1,0) OVER (ORDER BY PERIOD) *(POWER(POWER(1+@R * @F/12e+00, 12e+00/@F), wct.YEARFRAC(LAG(PaymentDate,1,NULL) OVER (ORDER BY PERIOD),PaymentDate,2)) - 1) As AI
FROM
mycte
)n
This produces the following result.
I
----------------------
3029.18926565336
The following SQL tells us why this is wrong.
;WITH mycte as (
SELECT
0 as Period,
@date_start as PaymentDate,
@P as Principal
UNION ALL
SELECT
Period + 1,
CAST(wct.EOMONTH(PaymentDate, 1) as date),
Principal
FROM
mycte
WHERE
PaymentDate < @date_end
)
SELECT
SUM(AI) as I,
SUM(InterestFactor) as [Sum of Interest Factors],
wct.PRODUCT(1 + InterestFactor) - 1 as [Product of Interest Factors],
(POWER(POWER((1+@R*@F/12),12/@F),wct.YEARFRAC(@date_start,@date_end,@basis))-1) as [Period Interest Factor]
FROM (
SELECT
*,
(POWER(POWER(1+@R * @F/12e+00, 12e+00/@F), wct.YEARFRAC(LAG(PaymentDate,1,PaymentDate) OVER (ORDER BY PERIOD),PaymentDate,2)) - 1) as InterestFactor,
LAG(Principal,1,0) OVER (ORDER BY PERIOD) *(POWER(POWER(1+@R * @F/12e+00, 12e+00/@F), wct.YEARFRAC(LAG(PaymentDate,1,NULL) OVER (ORDER BY PERIOD),PaymentDate,2)) - 1) As AI
FROM
mycte
)n
As you can see, the interest factor for the (six-month) period is not the sum of the monthly interest factors but is the product of (1 + monthly interest factors) - 1
|
I
|
Sum of Interest Factors
|
Product of Interest Factors
|
Period Interest Factor
|
|
3029.1893
|
0.030291893
|
0.030676790
|
0.030676790
|
Formulaically:
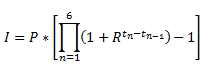
Where:
|
I
|
=
|
Interest Payment
|
|
P
|
=
|
Principal Amount
|
|
F
|
=
|
Frequency
|
|
n
|
=
|
Period
|
|
r
|
=
|
Interest Rate
|
|
R
|
=
|
(1 + (r*f/12)^(12/F)
|
|
tn
|
=
|
Time in years from period 0 to period n
|
We need to adjust our SQL so that it does more than just simply sum up the interest for each month. Essentially the monthly accrued interest that we calculated also needs to accrue interest until the next interest payment date. The following SQL shows one way to do that calculation.
;WITH mycte as (
SELECT
0 as Period,
@date_start as PaymentDate,
@P as Principal
UNION ALL
SELECT
Period + 1,
CAST(wct.EOMONTH(PaymentDate, 1) as date),
Principal
FROM
mycte
WHERE
PaymentDate < @date_end
)
SELECT
*,
AI * CIF as [Compounded],
SUM(AI*CIF) OVER (ORDER BY PERIOD ROWS UNBOUNDED PRECEDING) as Cumulative
FROM (
SELECT
*,
LAG(Principal,1,0) OVER (ORDER BY PERIOD) *(POWER(POWER(1+@R * @F/12e+00, 12e+00/@F), wct.YEARFRAC(LAG(PaymentDate,1,NULL) OVER (ORDER BY PERIOD),PaymentDate,2)) - 1) As AI,
POWER(POWER(1+@R * @F/12e+00, 12e+00/@F), wct.YEARFRAC(PaymentDate,@date_end,2))as CIF
FROM
mycte
)n
This produces the following result (which has been reformatted for ease of viewing).
|
Period
|
Payment
Date
|
Principal
|
AI
|
CIF
|
Compounded
|
Cumulative
|
|
0
|
2014-06-30
|
100000
|
0.000000
|
1.030677
|
0.000000
|
0.000000
|
|
1
|
2014-07-31
|
100000
|
510.366215
|
1.025443
|
523.351602
|
523.351602
|
|
2
|
2014-08-31
|
100000
|
510.366215
|
1.020236
|
520.694155
|
1044.045758
|
|
3
|
2014-09-30
|
100000
|
493.862203
|
1.015223
|
501.380037
|
1545.425794
|
|
4
|
2014-10-31
|
100000
|
510.366215
|
1.010067
|
515.504321
|
2060.930116
|
|
5
|
2014-11-30
|
100000
|
493.862203
|
1.005104
|
496.382709
|
2557.312825
|
|
6
|
2014-12-31
|
100000
|
510.366215
|
1.000000
|
510.366215
|
3067.679039
|
Now that we have figured out how to break in the interest payment calculation into sub-periods, accounting for the reduction in the principal balance is pretty simple.
DECLARE @P as money = 100000
DECLARE @date_start as date = '2014-06-30'
DECLARE @date_end as date = '2014-12-31'
DECLARE @R as float = 0.06
DECLARE @basis as int = 2 --Actual/360
DECLARE @F as int = 6
DECLARE @ppmt as money = 1000 --Principal Payment Amount
;WITH mycte as (
SELECT
0 as Period,
@date_start as PaymentDate,
@P as Principal
UNION ALL
SELECT
Period + 1,
CAST(wct.EOMONTH(PaymentDate, 1) as date),
--Principal
Principal - @ppmt
FROM
mycte
WHERE
PaymentDate < @date_end
)
SELECT
*,
AI * CIF as [Compounded],
SUM(AI*CIF) OVER (ORDER BY PERIOD ROWS UNBOUNDED PRECEDING) as Cumulative
FROM (
SELECT
*,
LAG(Principal,1,0) OVER (ORDER BY PERIOD) *(POWER(POWER(1+@R * @F/12e+00, 12e+00/@F), wct.YEARFRAC(LAG(PaymentDate,1,NULL) OVER (ORDER BY PERIOD),PaymentDate,2)) - 1) As AI,
POWER(POWER(1+@R * @F/12e+00, 12e+00/@F), wct.YEARFRAC(PaymentDate,@date_end,2))as CIF
FROM
mycte
)n
Of course, our CTE is only attempting to mimic the calculation of the first interest payments. It does not contain any logic for calculating the interest payment dates nor for clearing out the cumulative interest amounts on the interest payment dates. But, it's quite useful for understanding how a single interest payment account was calculated. It produces the following result.
|
Period
|
Payment
Date
|
Principal
|
AI
|
CIF
|
Compounded
|
Cumulative
|
|
0
|
2014-06-30
|
100000
|
0.000000
|
1.030677
|
0.000000
|
0.000000
|
|
1
|
2014-07-31
|
99000
|
510.366215
|
1.025443
|
523.351602
|
523.351602
|
|
2
|
2014-08-31
|
98000
|
505.262553
|
1.020236
|
515.487214
|
1038.838816
|
|
3
|
2014-09-30
|
97000
|
483.984959
|
1.015223
|
491.352436
|
1530.191252
|
|
4
|
2014-10-31
|
96000
|
495.055228
|
1.010067
|
500.039192
|
2030.230444
|
|
5
|
2014-11-30
|
95000
|
474.107715
|
1.005104
|
476.527401
|
2506.757844
|
|
6
|
2014-12-31
|
94000
|
484.847904
|
1.000000
|
484.847904
|
2991.605748
|
This is easily compared to the calculation in ConstantPrincipalAmount
SELECT TOP 7
Period,
PaymentDate,
CapitalAmountInDebt as Principal,
PrincipalPayment,
InterestPayment
FROM wct.ConstantPrincipalAmount(
100000 --@OutstandingAmount
,'Actual/360' --@InterestBasis
,.06 --@InterestRate
,1 --@FreqPayPrincipal
,6 --@FreqPayInterest
,1000 --@PrinPayAmount
,'2014-06-30' --@ReferenceDate
,NULL --@PrevPrincipalPayDate
,NULL --@PrevInterestPayDate
,NULL --@StartDate
,NULL --@FirstPrincipalPayDate
,NULL --@FirstInterestPayDate
,NULL --@PrincipalGracePeriodStartDate
,NULL --@PrincipalGracePeriodEndDate
,NULL --@InterestGracePeriodStartDate
,NULL --@InterestGracePeriodEndDate
)
which produces the following result.
|
Period
|
PaymentDate
|
Principal
|
PrincipalPayment
|
InterestPayment
|
|
0
|
6/30/2014
|
100000
|
0
|
0.000000
|
|
1
|
7/31/2014
|
99000
|
1000
|
0.000000
|
|
2
|
8/31/2014
|
98000
|
1000
|
0.000000
|
|
3
|
9/30/2014
|
97000
|
1000
|
0.000000
|
|
4
|
10/31/2014
|
96000
|
1000
|
0.000000
|
|
5
|
11/30/2014
|
95000
|
1000
|
0.000000
|
|
6
|
12/31/2014
|
94000
|
1000
|
2991.605748
|
Grace Interest
Grace interest is the extra interest that is accrued during a grace period. A grace period can occur at the very start of the loan when, for example, the first interest payment isn't due for a year but all the subsequent interest payments are to be made quarterly. Grace interest should not be confused with interest forgiveness as interest is still accrued during the grace period and the full amount of accrued interest is due at the first interest payment date or the grace period end date.
Grace Interest can also occur at some point during the life of the loan as specified by a grace period start date and a grace period end date. Again, the grace interest amount is the difference between the total interest accrued during the grace period and the amount of interest that would have been accrued if the period were of normal length.
In both cases, the grace interest is really an allocation of the interest that is accrued during the grace period. Thus, the calculation of the grace interest amount is a three-step process. First, calculate the total interest for the grace period. Second, calculate the interest for the last n months of the grace period, where n is the interest payment frequency. Third, subtract that amount from the total interest for the period.
In SQL terms we could look at the grace interest calculation as something like this.
DECLARE @P as money = 100000
DECLARE @date_start as date = '2014-06-30'
DECLARE @date_firstpay as date = '2015-03-31'
DECLARE @R as float = 0.06
DECLARE @basis as int = 2 --Actual/360
DECLARE @F as int = 3
SELECT
*,
I-R as [Grace Interest]
FROM (
SELECT @P*(POWER(POWER((1+@R*@F/12),12/@F),wct.YEARFRAC(@date_start,@date_FirstPay,@basis))-1) as I,
@P*(POWER(POWER((1+@R*@F/12),12/@F),wct.YEARFRAC(wct.EOMONTH(@date_FirstPay, -@F),@date_FirstPay,@basis))-1) as R
)n
This produces the following result.
|
I
|
R
|
Grace Interest
|
|
4637.05462126520
|
1499.99999999999
|
3137.05462126521
|
We can use the Balloon function to verify this calculation.
SELECT TOP 2
Period,
PaymentDate,
CapitalAmountInDebt,
InterestPayment,
GraceInterest
FROM wct.Balloon(
100000 --@OutstandingAmount
,'Actual/360' --@InterestBasis
,.06 --@InterestRate
,3 --@PaymentFrequency
,'2019-06-30' --@MaturityDate
,'2014-06-30' --@ReferenceDate
,NULL --@PrevPayDate
,NULL --@StartDate
,'2015-03-31' --@FirstPayDate
,NULL --@GracePeriodStartDate
,NULL --@GracePeriodEndDate
)
This produces the following result.
|
Period
|
PaymentDate
|
CapitalAmountInDebt
|
InterestPayment
|
GraceInterest
|
|
0
|
6/30/2014
|
100000
|
0
|
0
|
|
1
|
3/31/2015
|
100000
|
1500
|
3137.05462
|
We can modify the SQL that we used to calculate the accrued interest for each month in the grace period (see above) to calculate the interest payment amount and the grace interest amount. We will need to use the PaymentPeriods function to determine the first payment date.
DECLARE @P as money = 100000
DECLARE @date_start as date = '2014-06-30'
DECLARE @date_firstpay as date = '2015-03-31'
DECLARE @R as float = 0.06
DECLARE @basis as int = 2 --Actual/360
DECLARE @F as int = 6
DECLARE @period_firstpay as int =(
SELECT
MonthsUntilFirstPayment
FROM
wct.PAYMENTPERIODS(
@date_start,
@F,
NULL,
NULL,
@date_firstpay,
NULL,
NULL,
NULL
)
)
;WITH mycte as (
SELECT
0 as Period,
@date_start as PaymentDate,
@P as Principal
UNION ALL
SELECT
Period + 1,
CAST(wct.EOMONTH(PaymentDate, 1) as date),
Principal
FROM
mycte
WHERE
PaymentDate < @date_firstpay
)
SELECT
*,
SUM([Grace Interest]) OVER (ORDER BY PERIOD ROWS UNBOUNDED PRECEDING) as [Cum Grace Interest],
SUM([Interest Payment]) OVER (ORDER BY PERIOD ROWS UNBOUNDED PRECEDING) as [Cum Interest Payment]
FROM (
SELECT
Period,
PaymentDate,
Principal,
CASE
WHEN PERIOD <= @period_firstpay - @F THEN AI
ELSE 0
END * CIF as [Grace Interest],
CASE
WHEN PERIOD <= @period_firstpay - @F THEN 0
ELSE AI
END * CIF as [Interest Payment]
FROM (
SELECT
*,
LAG(Principal,1,0) OVER (ORDER BY PERIOD) *(POWER(POWER(1+@R * @F/12e+00, 12e+00/@F), wct.YEARFRAC(LAG(PaymentDate,1,NULL) OVER (ORDER BY PERIOD),PaymentDate,2)) - 1) As AI,
POWER(POWER(1+@R * @F/12e+00, 12e+00/@F), wct.YEARFRAC(PaymentDate,@date_firstpay,2))as CIF
FROM
mycte
)n
)p
This produces the following result.
|
Period
|
Payment Date
|
Principal
|
Grace Interest
|
Interest Payment
|
Cum Grace Interest
|
Cum Interest Payment
|
|
0
|
2014-06-30
|
100000
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
|
1
|
2014-07-31
|
100000
|
531.143866
|
0.000000
|
531.143866
|
0.000000
|
|
2
|
2014-08-31
|
100000
|
528.446852
|
0.000000
|
1059.590719
|
0.000000
|
|
3
|
2014-09-30
|
100000
|
508.845162
|
0.000000
|
1568.435881
|
0.000000
|
|
4
|
2014-10-31
|
100000
|
0.000000
|
523.179746
|
1568.435881
|
523.179746
|
|
5
|
2014-11-30
|
100000
|
0.000000
|
503.773429
|
1568.435881
|
1026.953175
|
|
6
|
2014-12-31
|
100000
|
0.000000
|
517.965137
|
1568.435881
|
1544.918312
|
|
7
|
2015-01-31
|
100000
|
0.000000
|
515.335041
|
1568.435881
|
2060.253353
|
|
8
|
2015-02-28
|
100000
|
0.000000
|
463.214395
|
1568.435881
|
2523.467748
|
|
9
|
2015-03-31
|
100000
|
0.000000
|
510.366215
|
1568.435881
|
3033.833963
|
And now we adapt it for principal reductions during the grace period.
DECLARE @P as money = 100000
DECLARE @date_start as date = '2014-06-30'
DECLARE @date_firstpay as date = '2015-03-31'
DECLARE @R as float = 0.06
DECLARE @basis as int = 2 --Actual/360
DECLARE @F as int = 6
DECLARE @ppmt as money = 1000
DECLARE @period_firstpay as int =(
SELECT
MonthsUntilFirstPayment
FROM
wct.PAYMENTPERIODS(
@date_start,
@F,
NULL,
NULL,
@date_firstpay,
NULL,
NULL,
NULL
)
)
;WITH mycte as (
SELECT
0 as Period,
@date_start as PaymentDate,
@P as Principal
UNION ALL
SELECT
Period + 1,
CAST(wct.EOMONTH(PaymentDate, 1) as date),
Principal - @ppmt
FROM
mycte
WHERE
PaymentDate < @date_firstpay
)
SELECT
*,
SUM([Grace Interest]) OVER (ORDER BY PERIOD ROWS UNBOUNDED PRECEDING) as [Cum Grace Interest],
SUM([Interest Payment]) OVER (ORDER BY PERIOD ROWS UNBOUNDED PRECEDING) as [Cum Interest Payment]
FROM (
SELECT
Period,
PaymentDate,
Principal,
CASE
WHEN PERIOD <= @period_firstpay - @F THEN AI
ELSE 0
END * CIF as [Grace Interest],
CASE
WHEN PERIOD <= @period_firstpay - @F THEN 0
ELSE AI
END * CIF as [Interest Payment]
FROM (
SELECT
*,
LAG(Principal,1,0) OVER (ORDER BY PERIOD) *(POWER(POWER(1+@R * @F/12e+00, 12e+00/@F), wct.YEARFRAC(LAG(PaymentDate,1,NULL) OVER (ORDER BY PERIOD),PaymentDate,2)) - 1) As AI,
POWER(POWER(1+@R * @F/12e+00, 12e+00/@F), wct.YEARFRAC(PaymentDate,@date_firstpay,2))as CIF
FROM
mycte
)n
)p
This produces the following result.
|
Period
|
Payment Date
|
Principal
|
Grace Interest
|
Interest Payment
|
Cum Grace Interest
|
Cum Interest Payment
|
|
0
|
2014-06-30
|
100000
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
|
1
|
2014-07-31
|
99000
|
531.143866
|
0.000000
|
531.143866
|
0.000000
|
|
2
|
2014-08-31
|
98000
|
523.162384
|
0.000000
|
1054.306250
|
0.000000
|
|
3
|
2014-09-30
|
97000
|
498.668259
|
0.000000
|
1552.974509
|
0.000000
|
|
4
|
2014-10-31
|
96000
|
0.000000
|
507.484353
|
1552.974509
|
507.484353
|
|
5
|
2014-11-30
|
95000
|
0.000000
|
483.622492
|
1552.974509
|
991.106845
|
|
6
|
2014-12-31
|
94000
|
0.000000
|
492.066880
|
1552.974509
|
1483.173725
|
|
7
|
2015-01-31
|
93000
|
0.000000
|
484.414939
|
1552.974509
|
1967.588664
|
|
8
|
2015-02-28
|
92000
|
0.000000
|
430.789387
|
1552.974509
|
2398.378051
|
|
9
|
2015-03-31
|
91000
|
0.000000
|
469.536918
|
1552.974509
|
2867.914969
|
Which we can compare to the results returned by ConstantPrincipalRate.
SELECT TOP 10
Period,
PaymentDate,
CapitalAmountInDebt as Principal,
PrincipalPayment,
InterestPayment,
GraceInterest,
InterestRate
FROM wct.ConstantPrincipalRate(
100000 --@OutstandingAmount
,'Actual/360' --@InterestBasis
,.06 --@InterestRate
,1 --@FreqPayPrincipal
,6 --@FreqPayInterest
,.01 --@AmortizationRate
,1000 --@MinimumPaymnet
,'2014-06-30' --@ReferenceDate
,NULL --@PrevPrincipalPayDate
,NULL --@PrevInterestPayDate
,NULL --@StartDate
,NULL --@FirstPrincipalPayDate
,'2015-03-31' --@FirstInterestPayDate
,NULL --@PrincipalGracePeriodStartDate
,NULL --@PrincipalGracePeriodEndDate
,NULL --@InterestGracePeriodStartDate
,NULL --@InterestGracePeriodEndDate
)
This produces the following result.
|
Period
|
Payment Date
|
Principal
|
Principal
Payment
|
Interest
Payment
|
Grace
Interest
|
Interest
Rate
|
|
0
|
6/30/2014
|
100000
|
0
|
0.000000
|
0.000000
|
0.00000000
|
|
1
|
7/31/2014
|
99000
|
1000
|
0.000000
|
0.000000
|
0.00510366
|
|
2
|
8/31/2014
|
98000
|
1000
|
0.000000
|
0.000000
|
0.01023337
|
|
3
|
9/30/2014
|
97000
|
1000
|
0.000000
|
0.000000
|
0.01522253
|
|
4
|
10/31/2014
|
96000
|
1000
|
0.000000
|
0.000000
|
0.02040389
|
|
5
|
11/30/2014
|
95000
|
1000
|
0.000000
|
0.000000
|
0.02544327
|
|
6
|
12/31/2014
|
94000
|
1000
|
0.000000
|
0.000000
|
0.03067679
|
|
7
|
1/31/2015
|
93000
|
1000
|
0.000000
|
0.000000
|
0.03593702
|
|
8
|
2/28/2015
|
92000
|
1000
|
0.000000
|
0.000000
|
0.04071126
|
|
9
|
3/31/2015
|
91000
|
1000
|
2867.914969
|
1552.974509
|
0.04602270
|
Principal Payments
For Bullet and Balloon there is a single principal payment at the maturity of the loan.
For ConstantCashFlow the principal payment is the same as what would be calculated using the PPMT function. This SQL shows how the principal payment amount changes for each period.
DECLARE @P as float = 100000
DECLARE @date_start as date = '2014-06-30'
DECLARE @date_maturity as date = '2019-06-30'
DECLARE @R as float = 0.06
DECLARE @F as int = 3
DECLARE @num_pmts as int =(
SELECT
NumberOfPayments
FROM
wct.PaymentPeriods(
@date_start,
@F,
NULL,
@date_start,
NULL,
NULL,
NULL,
@date_maturity
)
)
;with mycte as (
SELECT
0 as Period,
@P as Principal,
0e+00 as PrincipalPayment
UNION ALL
SELECT
Period + 1,
Principal - wct.PPMT(@R*@F/12,Period + 1,@num_pmts,-@P,0,0),
wct.PPMT(@R*@F/12,Period + 1,@num_pmts,-@P,0,0)
FROM
mycte
WHERE
Period < @num_pmts
)
SELECT
*
FROM
mycte
This produces the following result.
|
Period
|
Principal
|
Principal Payment
|
|
0
|
100000.000000
|
0.000000
|
|
1
|
95675.426413
|
4324.573587
|
|
2
|
91285.984221
|
4389.442191
|
|
3
|
86830.700397
|
4455.283824
|
|
4
|
82308.587316
|
4522.113081
|
|
5
|
77718.642538
|
4589.944778
|
|
6
|
73059.848589
|
4658.793949
|
|
7
|
68331.172730
|
4728.675859
|
|
8
|
63531.566733
|
4799.605996
|
|
9
|
58659.966647
|
4871.600086
|
|
10
|
53715.292559
|
4944.674088
|
|
11
|
48696.448360
|
5018.844199
|
|
12
|
43602.321498
|
5094.126862
|
|
13
|
38431.782733
|
5170.538765
|
|
14
|
33183.685887
|
5248.096846
|
|
15
|
27856.867588
|
5326.818299
|
|
16
|
22450.147014
|
5406.720574
|
|
17
|
16962.325632
|
5487.821382
|
|
18
|
11392.186929
|
5570.138703
|
|
19
|
5738.496145
|
5653.690784
|
|
20
|
0.000000
|
5738.496145
|
You can use this SQL to obtain the same result from ConstantCashFlow.
SELECT
Period,
CapitalAmountInDebt as Principal,
PrincipalPayment
FROM wct.ConstantCashFlow(
100000 --@OutstandingAmount
,0 --@LastPrinPayAmount
,.06 --@InterestRate
,3 --@PaymentFrequency
,'2019-06-30' --@MaturityDate
,'2014-06-30' --@ReferenceDate
,NULL --@PrevPayDate
,NULL --@StartDate
,NULL --@FirstPayDate
,NULL --@GracePeriodStartDate
,NULL --@InterestGracePeriodEndDate
)
In this SQL we can see how entering a final payment affects the principal payment calculation.
DECLARE @P as float = 100000
DECLARE @date_start as date = '2014-06-30'
DECLARE @date_maturity as date = '2019-06-30'
DECLARE @R as float = 0.06
DECLARE @F as int = 3
DECLARE @FV as float = 50000 --Final Payment
DECLARE @num_pmts as int =(
SELECT
NumberOfPayments
FROM
wct.PaymentPeriods(
@date_start,
@F,
NULL,
@date_start,
NULL,
NULL,
NULL,
@date_maturity
)
)
;with mycte as (
SELECT
0 as Period,
@P as Principal,
0e+00 as PrincipalPayment
UNION ALL
SELECT
Period + 1,
CASE Period + 1
WHEN @num_pmts THEN 0
ELSE Principal - wct.PPMT(@R*@F/12,Period + 1,@num_pmts-1,-@P,@FV,0)
END,
CASE PERIOD + 1
WHEN @num_pmts THEN @FV
ELSE wct.PPMT(@R*@F/12,Period + 1,@num_pmts-1,-@P,@FV,0)
END
FROM
mycte
WHERE
Period < @num_pmts
)
SELECT
*
FROM
mycte
This produces the following result.
|
Period
|
Principal
|
Principal Payment
|
|
0
|
100000.000000
|
0.000000
|
|
1
|
97706.076494
|
2293.923506
|
|
2
|
95377.744136
|
2328.332358
|
|
3
|
93014.486792
|
2363.257344
|
|
4
|
90615.780589
|
2398.706204
|
|
5
|
88181.093792
|
2434.686797
|
|
6
|
85709.886693
|
2471.207099
|
|
7
|
83201.611488
|
2508.275205
|
|
8
|
80655.712154
|
2545.899333
|
|
9
|
78071.624331
|
2584.087823
|
|
10
|
75448.775190
|
2622.849141
|
|
11
|
72786.583313
|
2662.191878
|
|
12
|
70084.458557
|
2702.124756
|
|
13
|
67341.801929
|
2742.656627
|
|
14
|
64558.005452
|
2783.796477
|
|
15
|
61732.452029
|
2825.553424
|
|
16
|
58864.515303
|
2867.936725
|
|
17
|
55953.559527
|
2910.955776
|
|
18
|
52998.939414
|
2954.620113
|
|
19
|
50000.000000
|
2998.939414
|
|
20
|
0.000000
|
50000.000000
|
Here is how that looks in the ConstantCashFlow function.
SELECT
Period,
CapitalAmountInDebt as Principal,
PrincipalPayment
FROM wct.ConstantCashFlow(
100000 --@OutstandingAmount
,50000 --@LastPrinPayAmount
,.06 --@InterestRate
,3 --@PaymentFrequency
,'2019-06-30' --@MaturityDate
,'2014-06-30' --@ReferenceDate
,NULL --@PrevPayDate
,NULL --@StartDate
,NULL --@FirstPayDate
,NULL --@GracePeriodStartDate
,NULL --@InterestGracePeriodEndDate
)
Though it might not seem obvious, the existence of grace periods in ConstantCashFlow will not affect the calculation of the principal payment amounts.
ConstantPrincipal amortizes the loan principal on a straight-line basis over the life of the loan based on the number of principal payments.
DECLARE @P as money = 100000
DECLARE @date_start as date = '2014-06-30'
DECLARE @date_end as date = '2019-06-30'
DECLARE @F as int = 3
DECLARE @num_pmts as int =(
SELECT
NumberOfPayments
FROM
wct.PaymentPeriods(
@date_start,
@F,
NULL,
NULL,
NULL,
NULL,
NULL,
@date_end
)
)
SELECT
@P / @num_pmts as PrincipalPayment
This produces the following result.
PrincipalPayment
---------------------
5000.00
If a final payment is entered then the calculation needs to be modified.
DECLARE @P as money = 100000
DECLARE @date_start as date = '2014-06-30'
DECLARE @date_end as date = '2019-06-30'
DECLARE @F as int = 3
DECLARE @amt_last_pmt as money = 25000
DECLARE @num_pmts as int =(
SELECT
NumberOfPayments
FROM
wct.PaymentPeriods(
@date_start,
@F,
NULL,
NULL,
NULL,
NULL,
NULL,
@date_end
)
)
SELECT
(@P - @amt_last_pmt) /(@num_pmts - 1) as PrincipalPayment
This produces the following result.
PrincipalPayment
---------------------
3947.3684
We could also adjust our SQL to be a little more flexible and work in both cases.
SELECT
CASE @amt_last_pmt
WHEN 0 THEN @P / @num_pmts
ELSE (@P - @amt_last_pmt) /(@num_pmts - 1)
END as PrincipalPayment
The calculation of the principal payment for ConstantPrincipalAmount is simple since the principal payment amount is an input to the function. The principal payment amount is applied to the outstanding balance until the balance is zero. The final payment is the lesser of the supplied principal payment amount and the outstanding balance of the loan.
DECLARE @P as money = 100000
DECLARE @ppmt as money = 4833.33
;WITH mycte as (
SELECT
0 as Period,
@P as Principal,
CAST(0 as money) as PrincipalPayment
UNION ALL
SELECT
Period + 1,
CAST(wct.GREATEROF(0, Principal - @ppmt) as money),
CAST(wct.LESSEROF(Principal, @ppmt) as money)
FROM
mycte
WHERE
Principal > 0
)
SELECT
*
FROM
mycte
This produces the following result.
|
Period
|
Principal
|
Principal Payment
|
|
0
|
100000
|
0
|
|
1
|
95166.67
|
4833.33
|
|
2
|
90333.34
|
4833.33
|
|
3
|
85500.01
|
4833.33
|
|
4
|
80666.68
|
4833.33
|
|
5
|
75833.35
|
4833.33
|
|
6
|
71000.02
|
4833.33
|
|
7
|
66166.69
|
4833.33
|
|
8
|
61333.36
|
4833.33
|
|
9
|
56500.03
|
4833.33
|
|
10
|
51666.70
|
4833.33
|
|
11
|
46833.37
|
4833.33
|
|
12
|
42000.04
|
4833.33
|
|
13
|
37166.71
|
4833.33
|
|
14
|
32333.38
|
4833.33
|
|
15
|
27500.05
|
4833.33
|
|
16
|
22666.72
|
4833.33
|
|
17
|
17833.39
|
4833.33
|
|
18
|
13000.06
|
4833.33
|
|
19
|
8166.73
|
4833.33
|
|
20
|
3333.40
|
4833.33
|
|
21
|
0
|
3333.40
|
You can run the following SQL to get the same results out of ConstantPrincipalAmount.
SELECT
Period,
CapitalAmountInDebt as Principal,
PrincipalPayment
FROM wct.ConstantPrincipalAmount(
100000 --@OutstandingAmount
,NULL --@InterestBasis
,.06 --@InterestRate
,3 --@FreqPayPrincipal
,3 --@FreqPayInterest
,4833.33 --@PrinPayAmount
,'2014-10-01' --@ReferenceDate
,NULL --@PrevPrincipalPayDate
,NULL --@PrevInterestPayDate
,NULL --@StartDate
,NULL --@FirstPrincipalPayDate
,NULL --@FirstInterestPayDate
,NULL --@PrincipalGracePeriodStartDate
,NULL --@PrincipalGracePeriodEndDate
,NULL --@InterestGracePeriodStartDate
,NULL --@InterestGracePeriodEndDate
)
ConstantPrincipalRate allows you to specify an amortization rate which is applied to the outstanding principal balance in order to calculate the principal payment amount. It also requires a minimum payment amount which is used in figuring out when to terminate the cash flow projection. The following SQL demonstrates the calculation of the principal payments.
DECLARE @P as float = 100000
DECLARE @rate_amort as float = 0.2
DECLARE @min_pmt as float = 2500
;WITH mycte as (
SELECT
0 as Period,
@P as Principal,
CAST(0 as float) as PrincipalPayment
UNION ALL
SELECT
Period + 1,
CAST(wct.GREATEROF(0, Principal - cast(wct.GREATEROF(@min_pmt, @rate_amort * Principal) as float)) as float),
CAST(wct.LESSEROF(Principal, wct.GREATEROF(@min_pmt, @rate_amort * Principal)) as float)
FROM
mycte
WHERE
Principal > 0
)
SELECT
*
FROM
mycte
This produces the following result.
|
Period
|
Principal
|
Principal Payment
|
|
0
|
100000.000000
|
0.000000
|
|
1
|
80000.000000
|
20000.000000
|
|
2
|
64000.000000
|
16000.000000
|
|
3
|
51200.000000
|
12800.000000
|
|
4
|
40960.000000
|
10240.000000
|
|
5
|
32768.000000
|
8192.000000
|
|
6
|
26214.400000
|
6553.600000
|
|
7
|
20971.520000
|
5242.880000
|
|
8
|
16777.216000
|
4194.304000
|
|
9
|
13421.772800
|
3355.443200
|
|
10
|
10737.418240
|
2684.354560
|
|
11
|
8237.418240
|
2500.000000
|
|
12
|
5737.418240
|
2500.000000
|
|
13
|
3237.418240
|
2500.000000
|
|
14
|
737.418240
|
2500.000000
|
|
15
|
0.000000
|
737.418240
|
You could run the following SQL to get the same results out of ConstantPrincipalRate.
SELECT
Period,
CapitalAmountInDebt as Principal,
PrincipalPayment
FROM wct.ConstantPrincipalRate(
100000 --@OutstandingAmount
,NULL --@InterestBasis
,NULL --@InterestRate
,NULL --@FreqPayPrincipal
,NULL --@FreqPayInterest
,0.20 --@AmortizationRate
,2500.00 --@MinimumPayment
,'2012-10-01' --@ReferenceDate
,NULL --@PrevPrincipalPayDate
,NULL --@PrevInterestPayDate
,NULL --@StartDate
,NULL --@FirstPrincipalPayDate
,NULL --@FirstInterestPayDate
,NULL --@PrincipalGracePeriodStartDate
,NULL --@PrincipalGracePeriodEndDate
,NULL --@InterestGracePeriodStartDate
,NULL --@InterestGracePeriodEndDate
)
The ConstantPaymentAmount table-valued function has the payment amount as an input parameter. This payment amount is applied to the interest payment first and the remaining balance is then applied to the principal balance until the principal is reduced to zero. Even though the payment amount is entered, it is adjusted when there is an initial grace period or interim grace period to reflect the additional interest that arises as a result of the grace period.
DECLARE @P as float = 100000
DECLARE @R as float = 0.06
DECLARE @F as int = 3
DECLARE @amt_pmt as float = 6666.00
;WITH mycte as (
SELECT
0 as Period,
@P as Principal,
CAST(0 as float) as PrincipalPayment,
CAST(0 as float) as InterestPayment
UNION ALL
SELECT
Period + 1,
Principal - CAST(wct.LESSEROF(Principal, @amt_pmt - Principal * @R * @F/12) as float) as Principal,
CAST(wct.LESSEROF(Principal, @amt_pmt - Principal * @R * @F/12) as float) as PrincipalPayment,
Principal * @R * @F/12 as InterestPayment
FROM
mycte
WHERE
Principal > 0
)
SELECT
*,
PrincipalPayment + InterestPayment as CashFlow
FROM
mycte
This produces the following result.
|
Period
|
Principal
|
Principal Payment
|
Interest Payment
|
Cash Flow
|
|
0
|
100000.000000
|
0.000000
|
0.000000
|
0.000000
|
|
1
|
94834.000000
|
5166.000000
|
1500.000000
|
6666.000000
|
|
2
|
89590.510000
|
5243.490000
|
1422.510000
|
6666.000000
|
|
3
|
84268.367650
|
5322.142350
|
1343.857650
|
6666.000000
|
|
4
|
78866.393165
|
5401.974485
|
1264.025515
|
6666.000000
|
|
5
|
73383.389062
|
5483.004103
|
1182.995897
|
6666.000000
|
|
6
|
67818.139898
|
5565.249164
|
1100.750836
|
6666.000000
|
|
7
|
62169.411997
|
5648.727902
|
1017.272098
|
6666.000000
|
|
8
|
56435.953177
|
5733.458820
|
932.541180
|
6666.000000
|
|
9
|
50616.492474
|
5819.460702
|
846.539298
|
6666.000000
|
|
10
|
44709.739861
|
5906.752613
|
759.247387
|
6666.000000
|
|
11
|
38714.385959
|
5995.353902
|
670.646098
|
6666.000000
|
|
12
|
32629.101749
|
6085.284211
|
580.715789
|
6666.000000
|
|
13
|
26452.538275
|
6176.563474
|
489.436526
|
6666.000000
|
|
14
|
20183.326349
|
6269.211926
|
396.788074
|
6666.000000
|
|
15
|
13820.076244
|
6363.250105
|
302.749895
|
6666.000000
|
|
16
|
7361.377388
|
6458.698856
|
207.301144
|
6666.000000
|
|
17
|
805.798049
|
6555.579339
|
110.420661
|
6666.000000
|
|
18
|
0.000000
|
805.798049
|
12.086971
|
817.885019
|
You could run the following SQL to get the same results out of ConstantPaymentAmount.
SELECT
Period,
CapitalAmountInDebt as Principal,
PrincipalPayment,
InterestPayment,
CashFlow
FROM wct.ConstantPaymentAmount(
100000 --@OutstandingAmount
,NULL --@InterestBasis
,.06 --@InterestRate
,3 --@PaymentFrequency
,6666.00 --@PaymentAmount
,'2014-10-01' --@ReferenceDate
,NULL --@PrevPayDate
,NULL --@StartDate
,NULL --@FirstPayDate
,NULL --@GracePeriodStartDate
,NULL --@InterestGracePeriodEndDate
)
We think that these new table-valued functions are a great addition to the XLeratorDB/financial library. We hope that you found this article insightful in explaining the intricacies of the interest and principal calculations contained in these functions. This was certainly not an exhaustive treatment of all the things that you can do with these new functions.
To find out more, you should download the free 15-day trial today and try them out. You can find all the documentation and lots of examples right here at westclintech.com and you should be able to just paste the examples right into SSMS to find out how you can use these functions.