BlackScholesMertonPriceNGreeks
Updated: 31 Oct 2013
Use the table-valued function BlackScholesMertonPriceNGreeks to calculate the price and other derivatives of a European option using the Black-Scholes-Merton option pricing formula.
Syntax
SELECT *
FROM [wctOptions].[wct].[BlackScholesMertonPriceNGreeks] (
<@CallPut, nvarchar(4000),>
,<@AssetPrice, float,>
,<@StrikePrice, float,>
,<@TimeToMaturity, float,>
,<@RiskFreeRate, float,>
,<@DividendRate, float,>
,<@Volatility, float,>)
Arguments
@CallPut
identifies the option as being a call ('C') or a put ('P'). @CallPut is an expression of type nvarchar or of a type that can be implicitly converted to nvarchar.
@AssetPrice
the price of the underlying asset. @AssetPrice is an expression of type float or of a type that can be implicitly converted to float.
@StrikePrice
the exercise price of the option. @StrikePrice is an expression of type float or of a type that can be implicitly converted to float.
@TimeToMaturity
the time to expiration of the option, expressed in years. @TimeToMaturity is an expression of type float or of a type that can be implicitly converted to float.
@RiskFreeRate
the continuously compounded risk-free zero coupon rate over the life of the option. @RiskFreeRate is an expression of type float or of a type that can be implicitly converted to float.
@DividendRate
the continuously compounded dividend zero-coupon rate over the life of the option. For currency options, @DividendRate should be the foreign risk-free interest rate. @DividendRate is an expression of type float or of a type that can be implicitly converted to float.
@Volatility
the volatility of the relative price change of the underlying asset. @Volatility is an expression of type float or of a type that can be implicitly converted to float.
Return Type
RETURNS TABLE (
[Price] [float] NULL,
[Delta] [float] NULL,
[Gamma] [float] NULL,
[Theta] [float] NULL,
[Vega] [float] NULL,
[Rho] [float] NULL,
[Lambda] [float] NULL,
[GammaP] [float] NULL,
[DdeltaDtime] [float] NULL,
[DdeltaDvol] [float] NULL,
[DdeltaDvolDvol] [float] NULL,
[DgammaDvol] [float] NULL,
[DvegaDvol] [float] NULL,
[VegaP] [float] NULL,
[PhiRho2] [float] NULL,
[DgammaDspot] [float] NULL,
[DeltaX] [float] NULL,
[RiskNeutralDensity] [float] NULL,
[DvommaDvol] [float] NULL,
[DgammaDtime] [float] NULL,
[DvegaDtime] [float] NULL,
[ForwardPrice] [float] NULL,
[ForwardPoints] [float] NULL
Unless otherwise specified, the columns returned by BlackScholesMertonPriceNGreeks are measuring the sensitivity of the theorteical value of the option.
|
Column
|
Description
|
|
Price
|
The theoretical value of the option.
|
|
Delta
|
The sensitivity to small changes in the asset price; the first derivative of the option with respect to price.
|
|
Gamma
|
The rate of change in Delta with respect to small changes in the asset price; the second derivative of the option with respect to price.
|
|
Theta
|
The sensitivity to small changes in time; the first derivative of the option with respect to time.
|
|
Vega
|
The sensitivity to small changes in volatility; the first derivative of the option with respect to volatility.
|
|
Rho
|
The sensitivity to small changes in the risk-free rate; the first derivative of the option with respect to the risk-free rate.
|
|
Lambda
|
Delta multiplied by the asset price divided by the theoretical value. If the theoretical value is zero, then lambda is set to zero.
|
|
GammaP
|
Gamma multiplied by asset price divided by strike price.
|
|
DdeltaDtime
|
The instantaneous change in delta over the passage of time; the second derivative, once to asset price and once to time.
|
|
DdeltaDvol
|
The sensitivity of delta with respect to volatility; the second derivative, once to asset price and once to volatility.
|
|
DdeltaDvolDvol
|
The second derivative of delta with respect to volatility; the third derivative, once to asset price and twice to volatility.
|
|
DgammaDvol
|
The rate of change in gamma with respect to changes in volatility; the third derivative, twice to asset price and once to volatility.
|
|
DvegaDvol
|
The rate of change to vega as the volatility changes; the second derivative with respect to volatility.
|
|
VegaP
|
The percentage change in theoretical value for a 10 per cent change in volatility.
|
|
PhiRho2
|
The sensitivity to a change in the dividend yield (foreign interest rate for a currency option); the first derivative with respect to dividend yield.
|
|
DgammaDspot
|
The rate of change in gamma with respect to change in the asset price; the third derivative with respect to price.
|
|
DeltaX
|
The sensitivity to a change in the strike price; the first derivative with respect to strike price.
|
|
RiskNeutralDensity
|
The sensitivity of DeltaX; the second derivative with respect to strike price.
|
|
DvommaDvol
|
The sensitivity of DvegaDvol to changes in volatility; the third derivative, twice to asset price and once to volatility.
|
|
DgammaDtime
|
The sensitivity of Gamma to the passage of time; the third derivative, twice to asset price and once to time.
|
|
DvegaDtime
|
The sensitivity of Vega to the passage of time; the second derivative, once to volatility and once to time.
|
|
ForwardPrice
|
The value of the underlying asset at the expiration date of the option.
|
|
ForwardPoints
|
The difference between the ForwardPrice and the asset price.
|
Remarks
· @TimeToMaturity must be greater than zero (@TimeToMaturity > 0).
· @AssetPrice must be greater than zero (@AssetPrice > 0).
· @StrikePrice must be greater than zero (@StrikePrice > 0).
· @Volatility must be greater than zero (@Volatility > 0).
· If @DividendRate is NULL then @DividendRate = 0.
· If @RiskFreeRate is NULL then @RiskFreeRate = 0.
Example
Calculate the price and Greeks for a call option on 2012-09-04, expiring on 2012-12-15, with a current asset price of 99.5, a strike price of 100 and a volatility of .20. The risk free rate is 2% and the dividend rate is 0.5.
SELECT *
FROM wct.BlackScholesMertonPriceNGreeks(
'C' --Put/Call
,99.5 --Asset Price
,100 --Strike Price
,datediff(d,'2012-09-04','2012-12-15') / 365.0000 --Time-to-expiry
,.02 --Risk Free Rate
,.005 --Dividend Rate
,.20 --Volatility
) k
Here are the first few columns of the resultant table.

In this SELECT we un-pivot the columns returned by the function for ease of viewing the results.
SELECT n.*
FROM wct.BlackScholesMertonPriceNGreeks(
'C' --Put/Call
,99.5 --Asset Price
,100 --Strike Price
,datediff(d,'2012-09-04','2012-12-15') / 365.0000 --Time-to-expiry
,.02 --Risk Free Rate
,.005 --Dividend Rate
,.20 --Volatility
) k
CROSS APPLY(VALUES
('Price',Price)
,('Delta',Delta)
,('Gamma',Gamma)
,('Theta',Theta)
,('Vega',Vega)
,('Rho',Rho)
,('Lambda',Lambda)
,('GammaP',GammaP)
,('DdeltaDtime',DdeltaDtime)
,('DdeltaDvol',DdeltaDvol)
,('DdeltaDvolDvol',DdeltaDvolDvol)
,('DgammaDvol',DgammaDvol)
,('DvegaDvol',DvegaDvol)
,('VegaP',VegaP)
,('PhiRho2',PhiRho2)
,('DgammaDspot',DgammaDspot)
,('DeltaX',DeltaX)
,('RiskNeutralDensity',RiskNeutralDensity)
,('DvommaDvol',DvommaDvol)
,('DgammaDtime',DgammaDtime)
,('DvegaDtime',DvegaDtime)
,('ForwardPrice',ForwardPrice)
,('ForwardPoints',ForwardPoints)
)n([Return Value], Value)
This prodcues the following result.
Return Value Value
------------------ ----------------------
Price 4.15002801072982
Delta 0.517263007462764
Gamma 0.0378316108959817
Theta -0.022410582448993
Vega 0.209333286210361
Rho 0.132230118433953
Lambda 12.4017643036327
GammaP 0.0376424528415018
DdeltaDtime -0.000265884058435201
DdeltaDvol 0.00120640336138375
DdeltaDvolDvol -1.56126607450338E-05
DgammaDvol -0.00189675260903188
DvegaDvol -2.86185329331919E-05
VegaP 0.418666572420722
PhiRho2 -0.143827456785512
DgammaDspot -0.000542407991020922
DeltaX -0.473176412318152
RiskNeutralDensity 0.0374542405772943
DvommaDvol -1.55316913764812E-06
DgammaDtime 0.000187137587406527
DvegaDtime -0.101680055475941
ForwardPrice 99.9179575658694
ForwardPoints 0.417957565869372
In the following SELECT, we will populate a derived table with some option information and then calculate the price and select greeks for options contained therein. For demonstration purposes we have made lots of simplifying assumptions about the US and contra interest rates and the implied volatility. This just demonstrates the structure of the TSQL statement.
SET NOCOUNT ON
/*Create a temporary table to store data*/
CREATE TABLE #opt (
z char(1),
s money,
ex datetime,
vol money
)
/*Put data in the table*/
INSERT INTO #opt VALUES ('C',98,'2012-09-22',0.23)
INSERT INTO #opt VALUES ('P',99,'2012-09-22',0.15)
INSERT INTO #opt VALUES ('C',100,'2012-09-22',0.15)
INSERT INTO #opt VALUES ('C',101,'2012-09-22',0.21)
INSERT INTO #opt VALUES ('P',102,'2012-09-22',0.19)
INSERT INTO #opt VALUES ('P',98,'2012-10-20',0.18)
INSERT INTO #opt VALUES ('P',99,'2012-10-20',0.24)
INSERT INTO #opt VALUES ('C',100,'2012-10-20',0.21)
INSERT INTO #opt VALUES ('P',101,'2012-10-20',0.25)
INSERT INTO #opt VALUES ('P',102,'2012-10-20',0.25)
INSERT INTO #opt VALUES ('P',98,'2012-11-17',0.17)
INSERT INTO #opt VALUES ('C',99,'2012-11-17',0.24)
INSERT INTO #opt VALUES ('P',100,'2012-11-17',0.17)
INSERT INTO #opt VALUES ('P',101,'2012-11-17',0.25)
INSERT INTO #opt VALUES ('P',102,'2012-11-17',0.22)
INSERT INTO #opt VALUES ('C',98,'2012-12-22',0.21)
INSERT INTO #opt VALUES ('C',99,'2012-12-22',0.19)
INSERT INTO #opt VALUES ('C',100,'2012-12-22',0.21)
INSERT INTO #opt VALUES ('C',101,'2012-12-22',0.15)
INSERT INTO #opt VALUES ('P',102,'2012-12-22',0.22)
INSERT INTO #opt VALUES ('C',98,'2013-03-16',0.24)
INSERT INTO #opt VALUES ('C',99,'2013-03-16',0.17)
INSERT INTO #opt VALUES ('P',100,'2013-03-16',0.2)
INSERT INTO #opt VALUES ('C',101,'2013-03-16',0.19)
INSERT INTO #opt VALUES ('C',102,'2013-03-16',0.21)
INSERT INTO #opt VALUES ('P',98,'2013-03-22',0.16)
INSERT INTO #opt VALUES ('P',99,'2013-03-22',0.25)
INSERT INTO #opt VALUES ('P',100,'2013-03-22',0.23)
INSERT INTO #opt VALUES ('C',101,'2013-03-22',0.22)
INSERT INTO #opt VALUES ('P',102,'2013-03-22',0.16)
/*Select data*/
SELECT O.z
,O.s as Strike
,O.ex as exDate
,O.vol as Volatility
,Cast(k.Price as money) as Price
,Cast(k.Delta as money) as Delta
,Cast(k.Gamma as money) as Gamma
,Cast(k.Theta as money) as Theta
,Cast(k.Vega as money) as Vega
,Cast(k.Rho as money) as Rho
,Cast(k.Lambda as money) as Lambda
FROM #OPT O
CROSS APPLY wct.BlackScholesMertonPriceNGreeks(
O.z --Put/Call
,96.76 --Asset Price
,O.s --Strike Price
,datediff(d,'2012-09-04',O.ex) / 365.0000 --Time-to-expiry
,0.0569 --Risk Free Rate
,0.00284 --Dividend Rate
,O.vol --Volatility
) k
/*Clean up table*/
DROP TABLE #opt
For ease of reading, we have reformatted the results.
|
z
|
Strike
|
exDate
|
Volatility
|
Price
|
Delta
|
Gamma
|
Theta
|
Vega
|
Rho
|
Lambda
|
|
C
|
98
|
22-Sep-12
|
0.23
|
1.53
|
0.4318
|
0.0795
|
-0.0599
|
0.0845
|
0.0199
|
27.3097
|
|
P
|
99
|
22-Sep-12
|
0.15
|
2.519
|
-0.7224
|
0.104
|
-0.0193
|
0.072
|
-0.0357
|
-27.7503
|
|
C
|
100
|
22-Sep-12
|
0.15
|
0.3233
|
0.1861
|
0.0831
|
-0.0266
|
0.0576
|
0.0087
|
55.7059
|
|
C
|
101
|
22-Sep-12
|
0.21
|
0.4949
|
0.2007
|
0.0622
|
-0.038
|
0.0603
|
0.0093
|
39.2314
|
|
P
|
102
|
22-Sep-12
|
0.19
|
5.209
|
-0.878
|
0.0495
|
-0.0095
|
0.0434
|
-0.0445
|
-16.3094
|
|
P
|
98
|
20-Oct-12
|
0.18
|
2.7705
|
-0.524
|
0.0644
|
-0.0188
|
0.1367
|
-0.0674
|
-18.3014
|
|
P
|
99
|
20-Oct-12
|
0.24
|
4.1557
|
-0.5579
|
0.0479
|
-0.0267
|
0.1355
|
-0.0733
|
-12.989
|
|
C
|
100
|
20-Oct-12
|
0.21
|
1.8111
|
0.377
|
0.0526
|
-0.0349
|
0.1304
|
0.0437
|
20.1391
|
|
P
|
101
|
20-Oct-12
|
0.25
|
5.5468
|
-0.6411
|
0.0435
|
-0.0248
|
0.1283
|
-0.0852
|
-11.184
|
|
P
|
102
|
20-Oct-12
|
0.25
|
6.2355
|
-0.6817
|
0.0415
|
-0.0225
|
0.1225
|
-0.091
|
-10.5781
|
|
P
|
98
|
17-Nov-12
|
0.17
|
3.0416
|
-0.4937
|
0.0538
|
-0.0124
|
0.1737
|
-0.103
|
-15.7054
|
|
C
|
99
|
17-Nov-12
|
0.24
|
3.6374
|
0.4773
|
0.0381
|
-0.0344
|
0.1734
|
0.0863
|
12.696
|
|
P
|
100
|
17-Nov-12
|
0.17
|
4.1816
|
-0.5979
|
0.0522
|
-0.0101
|
0.1684
|
-0.1258
|
-13.8352
|
|
P
|
101
|
17-Nov-12
|
0.25
|
6.1555
|
-0.5896
|
0.0357
|
-0.0192
|
0.1693
|
-0.1281
|
-9.2677
|
|
P
|
102
|
17-Nov-12
|
0.22
|
6.3061
|
-0.6448
|
0.0388
|
-0.0139
|
0.1621
|
-0.1393
|
-9.8933
|
|
C
|
98
|
22-Dec-12
|
0.21
|
4.5827
|
0.5342
|
0.0358
|
-0.0272
|
0.21
|
0.1407
|
11.2803
|
|
C
|
99
|
22-Dec-12
|
0.19
|
3.6978
|
0.4944
|
0.0397
|
-0.0249
|
0.2108
|
0.1318
|
12.9366
|
|
C
|
100
|
22-Dec-12
|
0.21
|
3.6902
|
0.4642
|
0.0358
|
-0.0263
|
0.2099
|
0.1231
|
12.1709
|
|
C
|
101
|
22-Dec-12
|
0.15
|
2.0622
|
0.3874
|
0.0483
|
-0.0192
|
0.2024
|
0.1058
|
18.1769
|
|
P
|
102
|
22-Dec-12
|
0.22
|
6.7389
|
-0.596
|
0.0333
|
-0.0111
|
0.2046
|
-0.1923
|
-8.5574
|
|
C
|
98
|
16-Mar-13
|
0.24
|
7.4524
|
0.5698
|
0.0232
|
-0.0242
|
0.2759
|
0.2521
|
7.3984
|
|
C
|
99
|
16-Mar-13
|
0.17
|
5.0277
|
0.5422
|
0.0331
|
-0.0193
|
0.2786
|
0.2508
|
10.4339
|
|
P
|
100
|
16-Mar-13
|
0.2
|
5.826
|
-0.4822
|
0.0283
|
-0.0067
|
0.28
|
-0.2775
|
-8.0087
|
|
C
|
101
|
16-Mar-13
|
0.19
|
4.6921
|
0.4855
|
0.0298
|
-0.02
|
0.2801
|
0.2236
|
10.0126
|
|
C
|
102
|
16-Mar-13
|
0.21
|
4.8451
|
0.4667
|
0.0269
|
-0.0211
|
0.2793
|
0.2132
|
9.3202
|
|
P
|
98
|
22-Mar-13
|
0.16
|
3.7562
|
-0.4198
|
0.0341
|
-0.0046
|
0.2789
|
-0.2419
|
-10.8137
|
|
P
|
99
|
22-Mar-13
|
0.25
|
6.7686
|
-0.4484
|
0.0221
|
-0.0102
|
0.2823
|
-0.2734
|
-6.4099
|
|
P
|
100
|
22-Mar-13
|
0.23
|
6.7179
|
-0.4735
|
0.0242
|
-0.0086
|
0.284
|
-0.2864
|
-6.8206
|
|
C
|
101
|
22-Mar-13
|
0.22
|
5.6654
|
0.4987
|
0.0253
|
-0.022
|
0.2846
|
0.2322
|
8.5172
|
|
P
|
102
|
22-Mar-13
|
0.16
|
5.8302
|
-0.554
|
0.0345
|
-0.0025
|
0.2819
|
-0.324
|
-9.1938
|
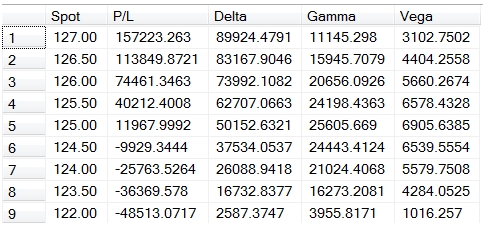
In this example, we translate some of the Greek values into monetary values in order to anticipate how changes in volatility, underlying, and time might affect the profit (or loss) on a long call position with a notional value of 10,000,000, which was bought at 0.50.
DECLARE @notional as float
DECLARE @position as float
SET @position = .50
SET @notional = 10000000
SELECT n.S as Spot
,CAST((k.Price - @position) * @notional/100 as money) as [P/L]
,CAST(k.Delta * @notional/100 as money) as Delta
,CAST(k.Gamma * @notional/100 as money) as Gamma
,CAST(k.Vega * @notional/100 as money) as Vega
FROM (
SELECT 122 UNION ALL
SELECT 123.50 UNION ALL
SELECT 124 UNION ALL
SELECT 124.50 UNION ALL
SELECT 125 UNION ALL
SELECT 125.5 UNION ALL
SELECT 126 UNION ALL
SELECT 126.50 UNION ALL
SELECT 127
) n(s)
CROSS APPLY wct.BlackScholesMertonPriceNGreeks('C'
,n.s --Asset price
,125 --Strike
,Cast(7 as float)/cast(365 as float) --Time
,0.000335699 --Continuously Compouned EURIBOR
,0.001869966 --Continuously Compouned LIBOR
,.09 --Volatility
) k
ORDER BY 1 DESC
This produces the following result